machine_learning记录

因为大创要整深度学习，没办法来学习一下机器学习和深度学习，当然只是学怎么用怎么调包调参，不会真有人搁那儿看数学吧，真的对这方面不是很感兴趣，学习一下怎么用就好了，以后要整再说

机器学习

特征工程

对于机器学习来说特征是很重要的，只有利用特征工程将特征进行提取，才能更好的将其用于机器学习模型的训练，很多时候特征工程才是提高机器学习准确率的重要步骤

对于特征工程，主要用到了sklearn库中的各个类及方法，对于中文的处理则用到了jieba中文分词库

特征抽取

count：

当数据以字典形式保存时使用sklearn.feature_extraction中的DictVectorizer类来进行处理，使用其中的fit_transform方法，可以得到一个经过处理的sparse矩阵，

当数据以列表方式存储时使用sklearn.feature_extraction.text中的 CountVectorizer类来进行处理，也是使用了fit_transform方法，

对于中文的句子，我们使用jieba分词库，让其按照一定的中文词语特性进行分词（对于英文是以空格来区分每个单词，对于中文则使用jieba来将句子中的词语间加上空格达到分词效果）

具体用法如下

from sklearn.feature_extraction import DictVectorizer
#特征抽取，导入包sklearn，Dicvectorizer是针对字典的特征处理类
from sklearn.feature_extraction.text import CountVectorizer
#对文本进行特征值化所用到的类
import jieba
def dicextra():
    """
    字典数据抽取
    :return: NONE
    """
    #实例化DictVectorizer对象
    dict=DictVectorizer();
    #调用fit_transform方法进行字典数据特征抽取
    data=dict.fit_transform([{'city':'北京','temperature':20},{'city':'上海','temperature':15},{'city':'成都','temperature':30}])
    #传入字典列表,返回sparse矩阵
    print(dict.feature_names_)
    print(data)
    return None

def textextra():
    """
    对文本进行特征值化
    :return: None
    """
    cv=CountVectorizer()
    #实例化对象
    data=cv.fit_transform(["this is not our life，life like this","This is about our future"])
    #传入的依然是可迭代的列表对象
    print(data.toarray())
    #将sparse矩阵转化为数组形式,进行标记，统计每一个词的出现次数(单个字母不统计)
    #中文默认不支持特征抽取，使用jieba进行分词，jieba返回词语生成器
    print(cv.get_feature_names())
    # 打印特征名称
def cut_chinese_worlds():
    """
    将中文句子利用jieba进行分词处理，返回列表，再将其转换为字符串，返回
    :return: c1,c2,c3
    """
    con1="最近对深度学习在视频任务中的应用做了个简单调研，切入点是视频目标检测，刚开始调研的时候很乐观，本想着作为研究课题继续研究，但是随着调研深入，到最后发现这个领域还是慎入，，，在这里把调研报告放出来吧。"
    con2="近些年来，深度卷积神经网络在图像目标检测领域迅速普及，而且相较于传统方法取得了很好的效果，基于深度学习的图像目标检测也逐渐合称为一个统一的深度网络框架。在图像目标检测任务取得了不错的效果后，深度学习又迁移到基于视频的目标检测任务上。"
    con3="目标检测是计算机视觉领域的一个经典的任务，是进行场景内容分析和理解等高级视觉任务的基本前提。视频中的目标检测任务更是和现实生活的需求贴近，现实生活中的智能视频监控、机器人导航等应用场景都需要对视频进行处理，对视频中的目标进行检测。"
    #字符串
    content1=jieba.cut(con1)
    content2 = jieba.cut(con2)
    content3 = jieba.cut(con3)
    #返回的值是生成器类型，需要对其进行转换
    contents1=list(content1)
    contents2 = list(content2)
    contents3 = list(content3)
    #转换为列表格式
    c1=' '.join(contents1)
    c2 = ' '.join(contents2)
    c3 = ' '.join(contents3)
    #转换为字符串
    return c1,c2,c3
def chinese_vec():
    """
    中文进行特征值化，使用jieba
    :return: None
    """
    c1,c2,c3=cut_chinese_worlds()
    #c1,c2,c3都是字符串
    cv=CountVectorizer()
    data=cv.fit_transform([c1,c2,c3])
    print(cv.get_feature_names())
    print(data.toarray())

if __name__=="__main__":
    chinese_vec()

但这并不是进行特征值抽取的常用方法，这样的方法是对词频进行统计，即一个词出现的次数进行统计，在对一些在各种文章中出现频率高的词语比如“我们”，进行统计的话，可能会造成将两篇并不想干的文章划分到一起，

tf-idf

tf：term frequency词频 ————-出现的次数

idf inverse document frequency 逆文档频率————–公式：log(总文档数量/该词出现的文档数)

重要性程度： tf*idf

tf-idf主要思想：如果某个词或短语在一篇文章中出现的频率高且在其它文章中出现较少，则认为此词具有很好的类别区分能力，适合用来分类。

tf-idf作用：用以评估一字词对于一个文件集或一个语料库中的期中一份文件的重要程度

使用sklearn.feaure_extraction.text.TFidfVectorizer类，

def tf_idf_tran():
    #进行tf-idf的特征值化
    c1,c2,c3=cut_chinese_worlds()
    tf=TfidfVectorizer()
    data=tf.fit_transform([c1,c2,c3])
    print(tf.get_feature_names())
    print(data.toarray())

这样就可以得到一个用tf-idf得到的sparse矩阵，但其数值就是重要性程度tf*idf

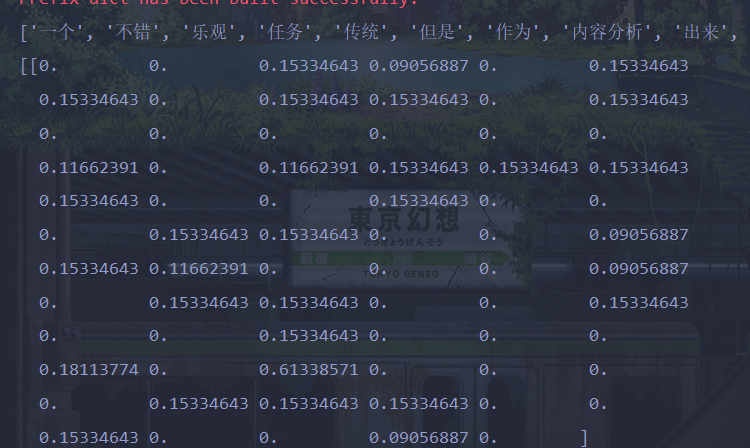
tf-idf是及机器学习特征处理的重要部

特征预处理

特征处理，通过特定的统计方法（数学方法）将数据转换成算法要求的数据对数据进行处理，两种特征预处理方式，一种是只对数据的特征大小进行修改，第二种事对特征的大小以及特征的数量进行修改

• 数值型数据：标准处理
  1. 归一化
  2. 标准化
  3. 缺失值
• 类别新数据：one-hot编码
  • one hot编码是将类别变量转换为机器学习算法易于利用的一种形式的过程。
    • 对于特征是类别的进行处理
• 时间类型：时间的切分

预处理API：都在sklearn.preprocessing中

归一化

特点：通过对原始数据进行变换把数据映射到（默认0-1）之间，公式：

使用API:sklearn.preprocessing.MinMaxScaler进行归一化处理，依然是先实例化MinMaxScaler再使用fit_transform进行转化

def mm():
    """
    预处理归一化
    :return: none
    """
    mm=MinMaxScaler()#添加参数feature_range=(2,3)即可让默认区间改为2-3
    #实例化
    data=mm.fit_transform([[89,3,45],[67,5,77],[100,7,55],[99,12,34]])
    print(data)
    return None

当多个特征同等重要时就使用归一化进行处理，因为不同特征之间差距可能很大，比如特征一的范围是一万至十万，而特征二的范围是一到十，若二者同等重要，不进行归一化处理直接进行计算会让特征二的值几乎可以忽略不计，所以使用归一化使二者的影响程度到达统一水平

归一化目的：使一个特征不会对最终结果造成更大影响

归一化缺点：对于异常点处理不是很好，异常点会对最大最小值造成很大影响，这种方法鲁棒性较差，只适合精确小数据场景（鲁棒性可简单理解为稳定性）

标准化

标准化使用了平均值，与方差，不容易受到异常点的影响

对于归一化，如果异常点影响了最大值和最小值，就会对结果产生显著的影响

对于标准化，具有一定的数据量，少量异常点对平均值影响较小，对方差影响较小

使用API：sklearn.preprosessing.StandardScaler,对数据进行处理

def ss():
    """
    预处理标准化,标准化缩放
    :return: None
    """
    ss=StandardScaler()
    #实例化
    data=ss.fit_transform([[89,3,45],[67,5,77],[100,7,55],[99,12,34]])
    print(data)

标准化总结：在样本较多 的情况下比较稳定，适合现代嘈杂大数据场景

归一化和标准化用于数值型的数据处理，但并非所有的算法都会用到归一化和标准化，会具体有所区别

缺失值处理

一般对缺失值处理是使用panda，但sklearn也有对确实值进行处理的模块，

对缺失值的处理一般有两种方法，删除和插补

• 删除：如果每行或列确实数据达到一定标准，选择放弃整行或整列
• 插补：对缺失值填补如该行，改列的平均值或中位数，（一般按列填补）

一般使用插补，因为如果数据不够多，删除数据会让数据更少

使用API：sklearn.preprossing.Imputer

在sklearn中缺失值的数据类型需要是np.nan(numpy)

imputetr类有三个参数，

• missing_value:缺失值，可以写成nan,NaN
• strategy：插补值，mean意味着填补平均数
• axis：以列或行填补，默认为0即列填补，1位行填补

numpy数组中可以使用np.nan(NaN)来代替缺失值，属于float类型

如果是文件中的一些缺失值，可以替换成nan，通过np.array转化成float型的数组即可

数据降维

维度：特征的数量，数据降维即减少特征的数量

特征选择

特征选择，即单纯的选择一部分的特征作为训练集特征，一些特征被舍去，特征在选择前或选择后可以改变值，也可以不改变值，但选择后的特征维数一定比之前小

特征选择的原因：

• 冗余：部分特征的相关度高，容易消耗计算性能
• 噪声：部分特征对预测结果有影响

特征选择主要方法：

• Filter(过滤式)：VarianceThreshold：对样本一特征的方差进行分析，指定方差的值进行筛选，即方差低于一定数值的特征会被删除，因为方差代表的该特征的稳定性，特征值过于接近就失去了分析的意义

  • 使用API：sklearn.feature_selection.VarianceThreshold

  

  def vt():
    """
    特征选择，过滤式，对方差进行过滤
    :return:None
    """
    vt=VarianceThreshold(threshold=1)
    #实例化，参数threshold表示将方差低于1的特征删去
    data=vt.fit_transform([[89,3,45],[67,3,77],[100,3,55],[99,3.1,34]])
    #返回一个特征减少了的数组
    print(data)
    return None

  threshold值需要依据具体情况来取

• Embedded(嵌入式)：正则化，决策树

• Wrapper(包裹式)（使用较少）

• 神经网络（有这样的功能，后续会记录到）

主成分分析(PCA)

使用API：sklearn.decomposition

PCA:是一种分析，简化数据集的技术，目的是为了数据维度的压缩，尽可能的降低原数据的维数（复杂度），损失少量数据，作用是可以消减回归分析或者聚类分析中的特征数量。应用场景并不多，当特征数量达到上百个时可以考虑用PCA，除了降低数据的维数，也会对数据进行更改

其中参数n_components有两种格式，一种是0-1的小数，代表保留特征的百分比，一般为0.9-0.95之间，另一种是整数，即保留多少个特征。

def pca():
    """
    主成分分析进行数据降维
    :return: None
    """
    pca=PCA(n_components=0.9)
    #实例化PCA,n_components=0.9代表保留百分之90的特征
    data=pca.fit_transform([[89,3,45],[67,3,77],[100,3,55],[99,3.1,34]])
    print(data)

    return None

当数据中有大量无效数据，比如如下场景：10000个顾客在超市中购买的物品，超市中的物品有1000种，因为每个顾客只会购买很少的物品，所以数据中会有大量的无效数据0存在，这时候就适合用主成分分析进行降维

机器学习基础

机器学习常用算法

数据类型很多时候是选择算法的依据，主要可分为两种，离散型数据，连续型数据

• 离散型数据：又称统计型数据，所有的这些数据都是整数型，不可再分的，比如有多少人，多少车，不能再细化细分来提高准确度
• 连续型数据：变量可以在一定范围内任取一数，如长度，质量等，是有小数部分的

机器学习开发流程：

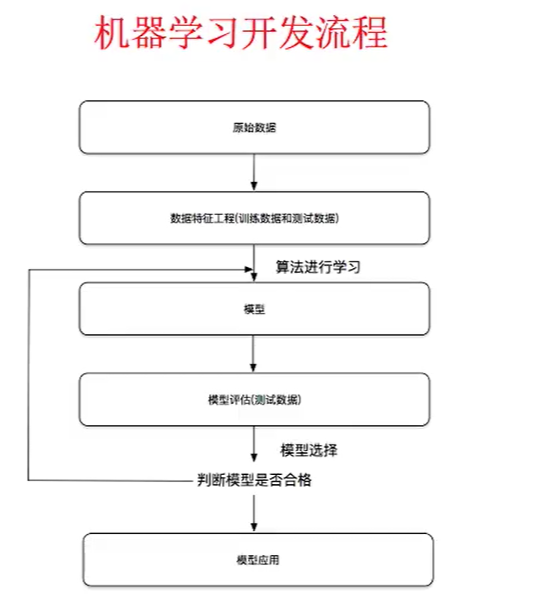
机器学习算法分类如下：

大体上分为监督学习和非监督学习，也有半监督学习的机器学习算法。（这里只列举了部分常用算法）

监督学习（预测）

监督学习是目前最常见的机器学习类型。给定一组样本（通常由人工标注），它可以学会将 输入数据映射到已知目标［也叫标注（annotation）］。其目标是学习训练输入与训 练目标之间的关系

有特征值，有目标值

• k-近邻算法
• 贝叶斯分类
• 决策树与随机森林

回归，对应连续型数值

• 逻辑回归
• 岭回归
• 标注 隐马尔可夫模型

自监督学习

自监督学习是监督学习的一个特例，自监督学习是没有 人工标注的标签的监督学习，可以将它看作没有人类参与的监督学习。标签仍然存在（因为 总要有什么东西来监督学习过程），但它们是从输入数据中生成的，通常是使用启发式算法生 成的。

无监督学习

只有特征值，无监督学习是指在没有目标的情况下寻找输入数据的有趣变换，其目的在于数据可视化、 数据压缩、数据去噪或更好地理解数据中的相关性。无监督学习是数据分析的必备技能，在解 决监督学习问题之前，为了更好地了解数据集，它通常是一个必要步骤。降维和聚类都是众所周知的无监督学习方法

聚类

• k-means

数据集的划分

拿到数据后并不是将所有的数据用于模型的训练，所以数据会分为训练集和测试集，训练集用于训练模型，测试集用于评估模型，比例可以设为7:3,8:2,7.5:2.5,

用于划分数据集的API：sklearn.model_selection.train_test_split，在进行数据划分前首先要进行数据的获取，也是使用到了sklearn中的api

x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)

返回四个值，分别为训练集特征值，测试集特征值，训练集的目标值，测试集的目标值，

参数x为特征值，y为目标值，test_size为测试集的比例，一般取0.25

转换器与估计器

在调用fit()输入数据后就可以使用估计器中的方法来进行分类和回归

• fit传入x_train,y_train及传入训练集的数据，具体用法以knn为例

knn= KNeighborsClassifier(n_neighbors=)#实例化
   #传入训练集特征值和目标值
   knn.fit(x_train,y_train)
   y_predict=knn.predict(x_test)#预测，传入的测试集特征值进行预测，返回预测的特征值
   print("预测的位置",y_predict)
   print("预测准确率",knn.score(x_test,y_test))#进行预测，传入测试集的目标值和预测值进行比较，得到准确率

常用分类算法基础

KNN–k近邻算法

选择最近的“邻居”作为分类依据

求“距离”就是本算法的核心

注意，在进行距离计算时需要先进行标准化处理

API：sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm=’auto’)

一个简单的完整knn开发流程如下：

导入数据–处理数据–数据分割–标准化–算法预测–后续调整

import pandas as pd
from sklearn.neighbors import KNeighborsClassifier  #knn算法api
from sklearn.model_selection import train_test_split    #数据分隔
import sklearn.decomposition    #主成分分析
from sklearn.preprocessing import StandardScaler    #标准化
pd.set_option('display.max_columns', None)
#pandas展示所有列
def knn():
    """
    knn算法预测入驻位置
    :return: None
    """
    #读入数据
    #使用pandas读入csv文件
    data = pd.read_csv('./data/train.csv')
    #进行测试，打印前10条
    # print(data.head(10))
    #处理数据
    #1.缩小数据量，使用pandas中的query
    data=data.query("x > 1.0 & x < 2.0 & y > 1.0 & y < 2.0")
    #2.对时间进行处理，使用pandas中的to_datetime实现,必须有返回值,返回时间格式的数据datetime
    time_value = pd.to_datetime(data['time'], unit='s')
    # print(time_value)
    # 通过对处理过的时间戳数据进行处理，提取出新的特征，构造出新的特征
    #使用datetimeindex进行处理，将时间格式的数据转化为字典格式,可以直接获取年月日等数据
    time_value = pd.DatetimeIndex(time_value)
    # 加入特征
    data['day']=time_value.day
    # data['year']=time_value.year
    data['month']=time_value.month
    data['hour']=time_value.hour
    data['weekday']=time_value.weekday
    #删除时间戳特征，使用drop,删除time,axis=1代表以列删除
    data.drop(['time'],axis=1)
    # print(data)
    #进行筛选，将入住人数少的place_id去掉
    #返回一个以place_id进行groupby后的数据流,输出的place_count后的剩余列会被count的数值所取代，完成了计数的目的
    #所以这里只用place_id和后面的数量进行筛选就好了
    place_count=data.groupby('place_id').count()
    #将少于3人入住的样本去掉，并重设索引，place_count是以place_id为索引
    #tf以通过reset_index()让其以之前的模式以row_id0,1,2,3。。。为索引
    tf=place_count[place_count.row_id>3].reset_index()
    # 对data进行筛选，以place_id为条件
    #使用了DateFrame中布尔索引，可以用满足布尔条件的列值来过滤数据
    data=data[data['place_id'].isin(tf.place_id)]
    #取出数据当中的特征值和目标值
    #设定特征值和目标值
    #特征值x
    x=data.drop(['place_id','row_id'],axis=1)
    #目标值y
    y=data['place_id']


    #数据分割
    x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
    #特征工程
    std=StandardScaler()
    x_train=std.fit_transform(x_train)
    x_test=std.fit_transform(x_test)
    #利用算法进行训练
    #实例化，与k=5
    knn= KNeighborsClassifier(n_neighbors=)
    #传入训练集特征值和目标值
    knn.fit(x_train,y_train)
    y_predict=knn.predict(x_test)
    print("预测的位置",y_predict)
    print("预测准确率",knn.score(x_test,y_test))
    return None

if __name__=="__main__":
    knn()

在完成一次流程开发后需要做的就是提升精度，主要就是调参了，比如对k的值进行改变，对test_size进行改变

朴素贝叶斯算法

划分类别的基本思想：对其分类做概率预测，预测得到的概率最高的一项就是其分类的最终结果

需要用到条件概率，而条件概率的使用条件是事件要相互独立，在B的条件下A的概率即P(A|B),B的条件下a1,a2的概率：P(a1,a2|B)=P(a1|B)*P(a2|B),

所以朴素贝叶斯的使用场景是特征值相互独立

朴素贝叶斯公式：

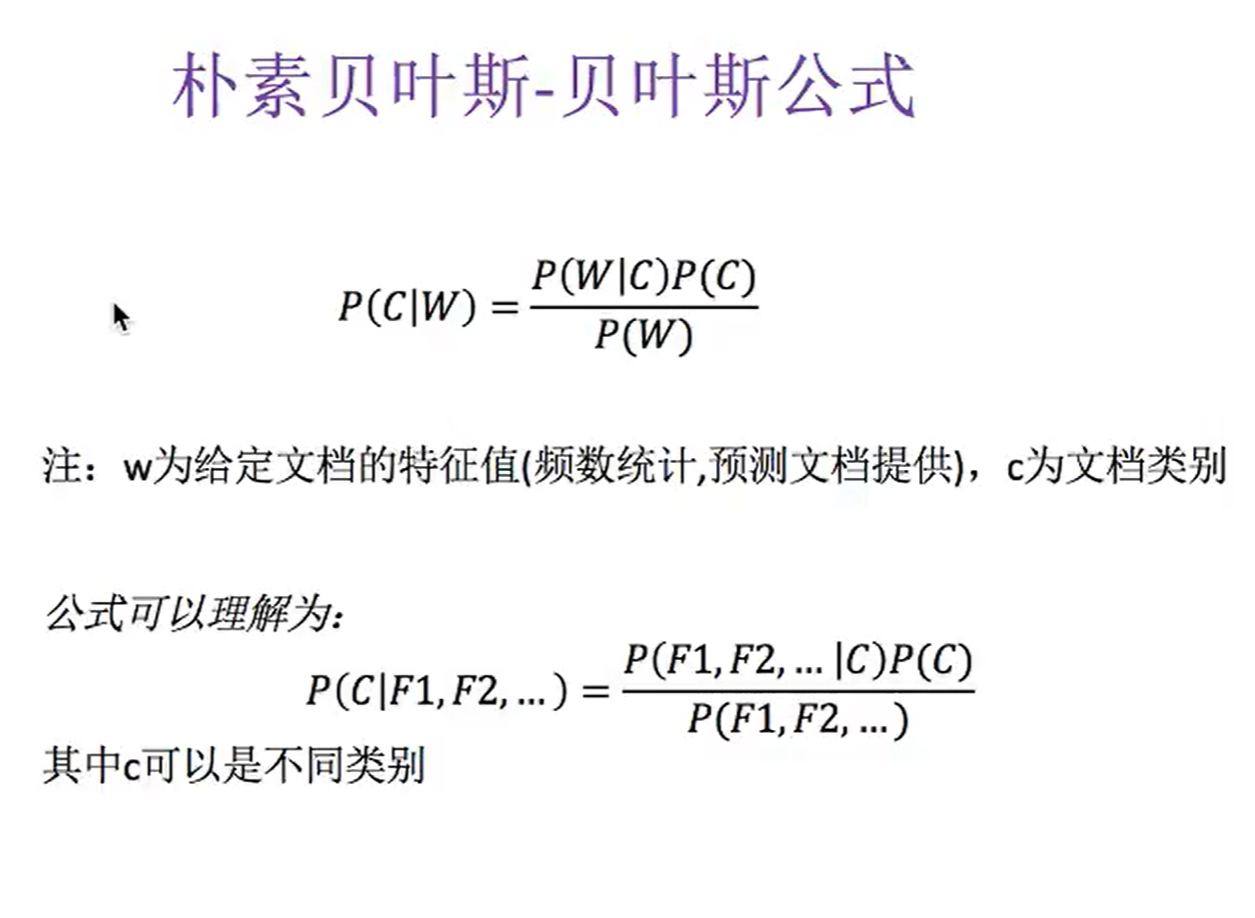
我们要求的就是在给出文档的特征的条件下，求出他是一类类别的概率，如上图所示

但有时候会出现概率为0的情况，比如一个词从未出现在一类文章中

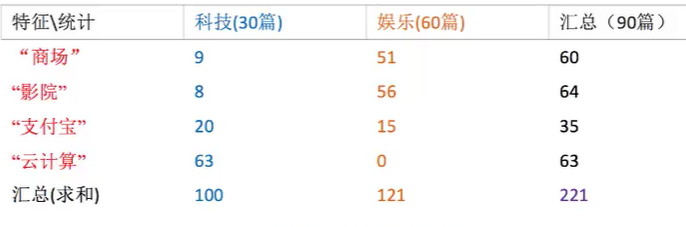
云计算从来没出现在娱乐中过，此时一篇待预测文档出现了商场，影院，云计算这几个关键词，这时候求的P(云计算|娱乐)=0/121=0,那P(W|娱乐)直接为0了，但这样显然存在问题

解决方法：加入拉普拉斯平滑系数

简单来说就是P(F1|C)=Ni/N变为Ni+a/N+a*m，即加上一个系数，a一般为1，m为特征词的个数，上图共有4个特征词，即商场，影院，支付宝，云计算。

API：sklearn.naive_bayes.MultinomialNB

朴素贝叶斯算法受训练及影响非常大

import pandas as pd
from sklearn.neighbors import KNeighborsClassifier  #knn算法api
from sklearn.model_selection import train_test_split    #数据分隔
import sklearn.decomposition    #主成分分析
from sklearn.preprocessing import StandardScaler    #标准化
from sklearn.datasets import fetch_20newsgroups#数据导入
from sklearn.naive_bayes import MultinomialNB   #朴素贝叶斯
from sklearn.feature_extraction.text import TfidfVectorizer #特征抽取
def naivebayes():
    """
    朴素贝叶斯对新闻分类
    :return:None
    """
    #读入数据,来自sklearn.datasets API
    news = fetch_20newsgroups(subset='all')
    #数据分割
    x_train,x_test,y_train,y_test=train_test_split(news.data,news.target,test_size=0.25)
    #特征抽取,tf-idf
    tf=TfidfVectorizer()
    x_train = tf.fit_transform(x_train)
    x_test = tf.transform(x_test)
    #特征工程，预处理标准化，这里不能使用特征工程。。。。
    # st=StandardScaler()
    # x_train=st.fit_transform(x_train)
    # x_test=st.fit_transform(x_test)
    #进行转化
    nb=MultinomialNB(alpha=1.0)
    nb.fit(x_train,y_train)
    y_predict = nb.predict(x_test)
    print("预测结果",y_predict)
    print("正确率",nb.score(x_test,y_test))

    return None

这是使用了sklearn中的20newsgroup进行朴素贝叶斯模型的一个对新闻分类的训练

• 分类模型的评估：

  包括了准确率，精确率，召回率

1. 准确率：estimator.score()，各种估计器都有的方法，用其来判断模型的准确率

混淆矩阵，在分类任务中，正确结果与标记之间存在四种不同的组合，构成了混淆矩阵，每一个分类都有自己的混淆矩阵

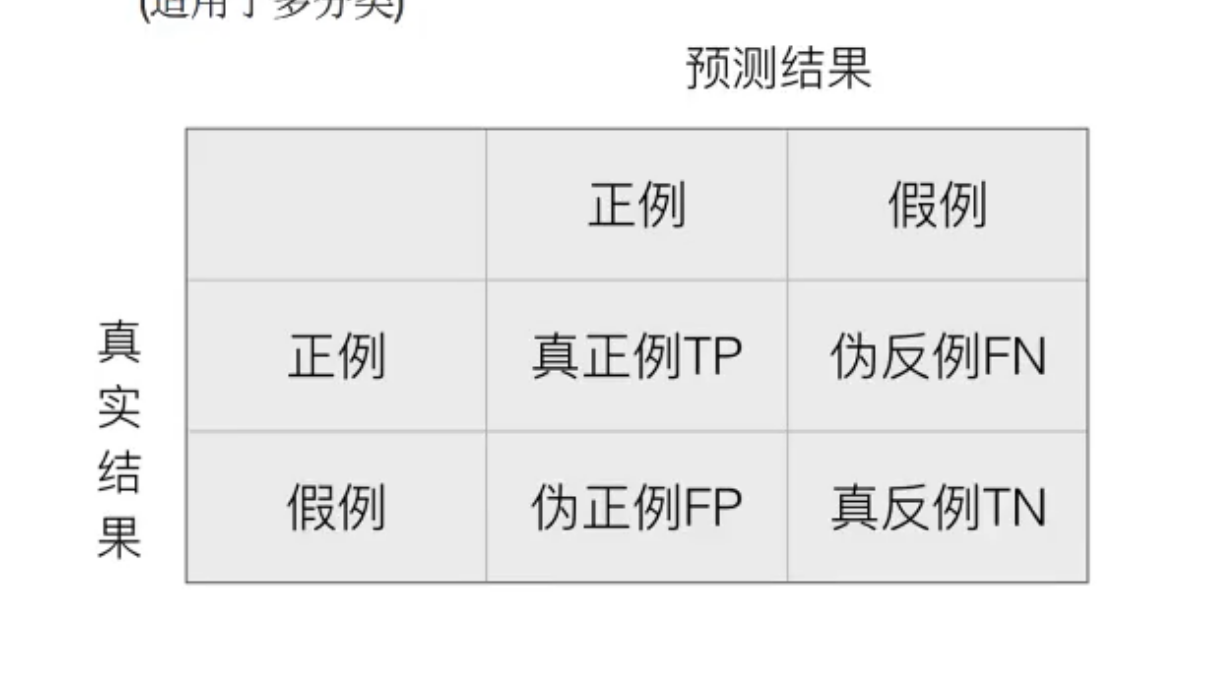
通过混淆矩阵，引出准确率和召回率

2. 精确率: 是正例的样本数为x,所有的样本数为z，对这z个样本进行预测后，有y个被预测为正例，这y个样本中共有k个在x中（k<=x)**则精确率为：k/y**
3. 召回率：是正例的样本数为x，对这x个样本进行进行预测后，有y个被预测为正例（y=<x)则召回率为y/x，应用较多
4. F1-score:反映了模型的稳健性

使用api：sklearn.metrics.classfication_report

这里使用上面的朴素贝叶斯算法做一个演示：

print("对模型的评估：",classification_report(y_test,y_predict,target_names=news.target_nam es))

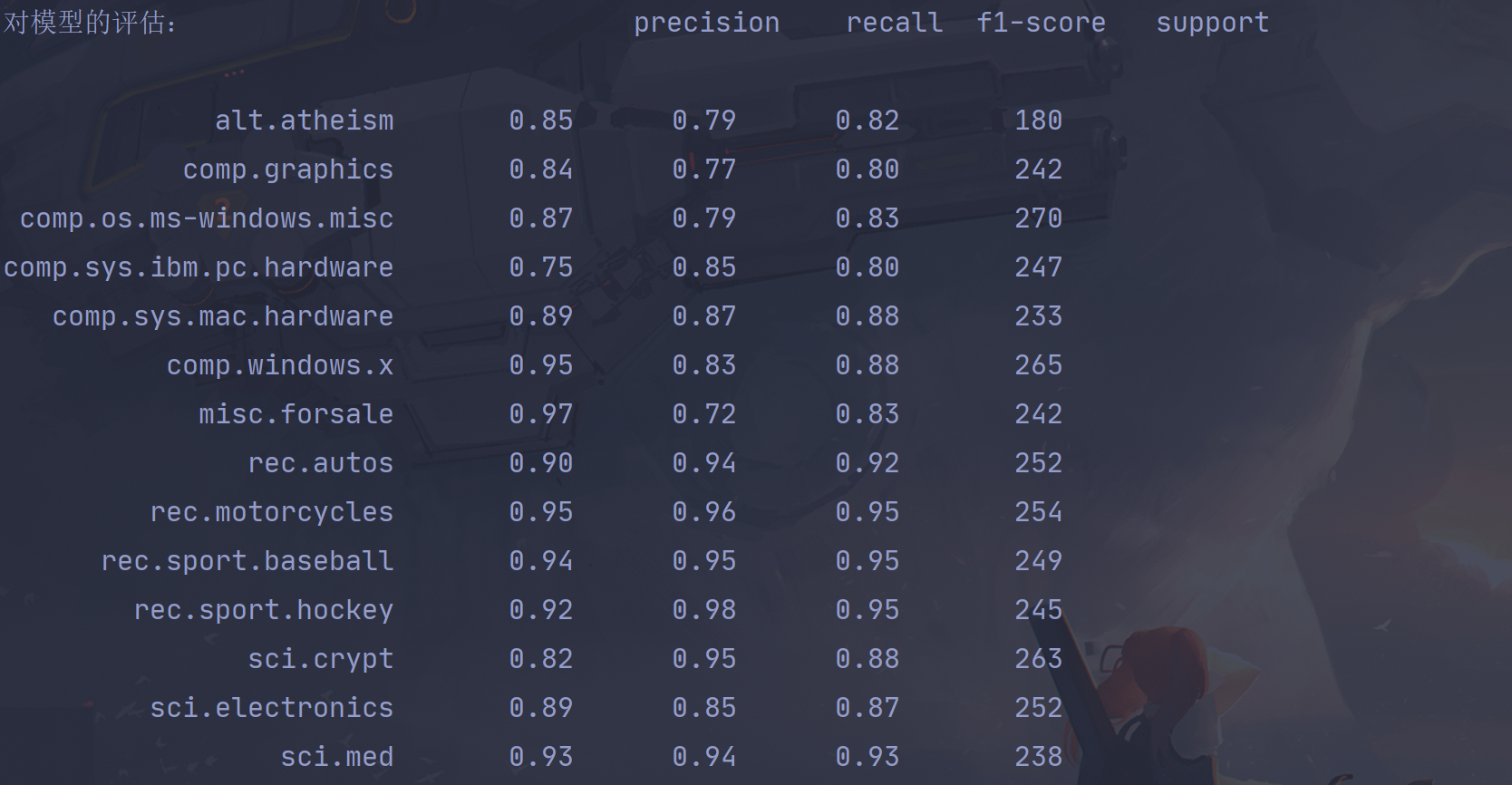
可以看到精确率，召回率，f1-score，support(划分为该类别的样本数量)

决策树与随机森林

决策树的初始起源很朴素，是一种if-then的判断过程

决策树的分类依据之一：信息增益，因为信息增益越大，表示得知该特征后分类不确定性减少越大

常见的使用决策树的算法：

决策树使用API：sklearn.tree.DecisionTreeClassifier

def dct():
    """
    决策树分析泰坦尼克号数据集
    :return: None
    """
    #读入数据
    data=pd.read_csv('./data/train.csv')
    #选取特征值和目标值
    x_titan=data[["Pclass","Sex","Age"]]
    y_titan=data["Survived"]
    # print(x_titan)
    #缺失值处理
    x_titan["Age"].fillna(x_titan["Age"].mean(),inplace=True)
    # print(x_titan)
    #数据集分割
    x_train,x_test,y_train,y_test=train_test_split(x_titan,y_titan,test_size=0.25)
    #数据处理，（特征工程）one-hot
    #将x_train中的数据转换为字典格式以便进行one-hot编码
    dicts = DictVectorizer(sparse=False)#实例化自带你类别处理器
    x_train=dicts.fit_transform(x_train.to_dict(orient="records"))#pd方法转化为一个样本对应的一个字典
    x_test=dicts.fit_transform(x_test.to_dict(orient="records"))
    print(dicts.get_feature_names())
    print(x_train)  #此时输出已经是one-hot转化后
    #决策树
    dec=DecisionTreeClassifier()
    dec.fit(x_train,y_train)
    #预测准确率
    print("预测准确率",dec.score(x_test,y_test))

随机森林：包含多个决策树的分类器，属于集成学习方法

随机森林的建立过程：

数据集中有N个样本，M个特征

1. 建立单个树：
   1. 随机在这N个样本中选取一个，重复随机选取N次重复随机代表被选取的样本中可能会有重复
   2. 随机从M个特征中选取m个（m<M)
   3. 按照这N个样本m个特征构成一个随机数
2. 循环上述过程，形成多个决策树

这多个决策树的样本，特征大多不一样

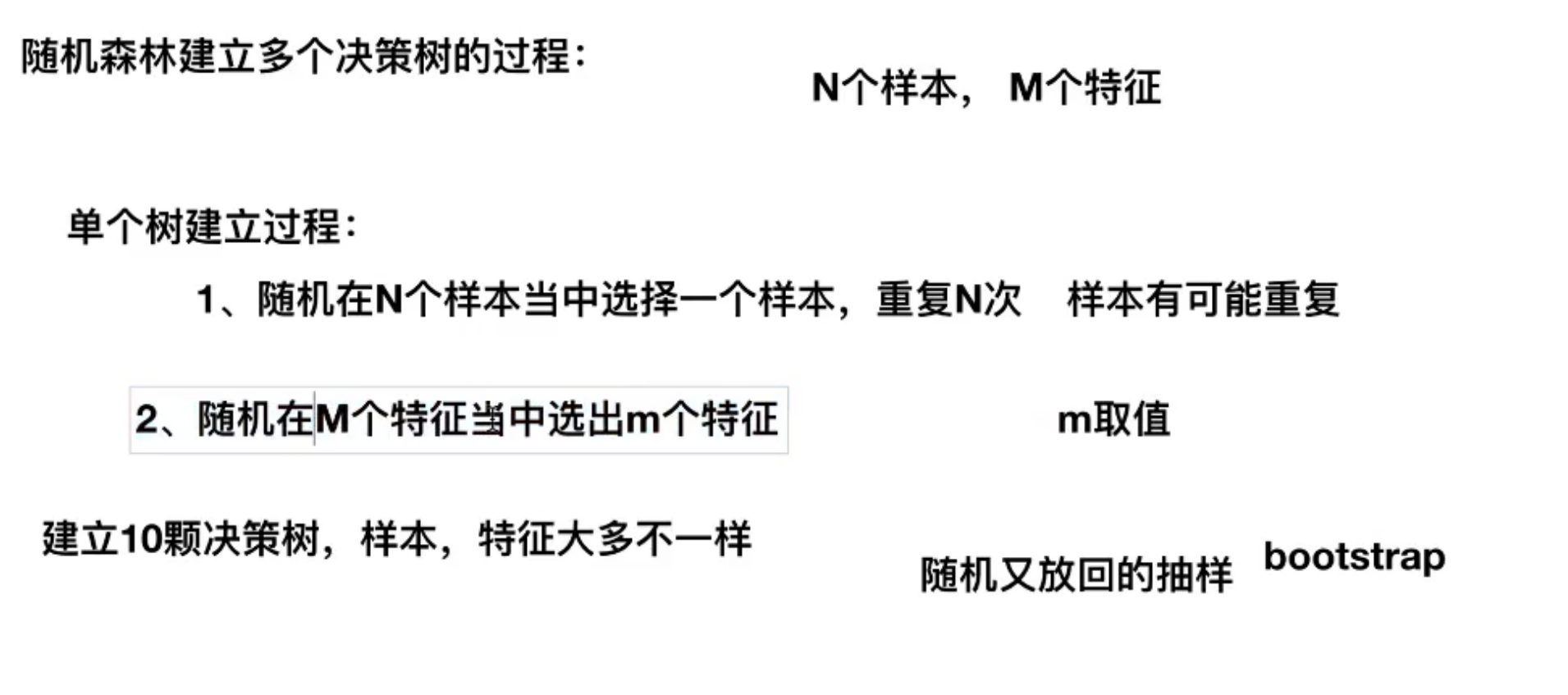
随机森林api：sklearn.ensemble.RandomForestVlassifier

#和决策树公用一个数据集，可以进行对比
rf=RandomForestClassifier()#随机森林实例化，不传入参数，进行网格搜索
   param_grid={"n_estimators":[120,150,200,300,500],"max_depth":[5,8,10]}
   # 实例化
   msgv=GridSearchCV(rf,param_grid,cv=3)
   msgv.fit(x_train,y_train)
   print("随机森林预测准确率",msgv.score(x_test,y_test))

模型的选择与调优

交叉验证

交叉验证的目的是为了让被评估的模型更加准确可信，交叉验证用于评估模型的预测性能，尤其是训练好的模型在新数据上的表现，可以在一定程度上减小过拟合。

简单的说交叉验证就是将训练集划分为几个大小相同的集合，这里以四个为例，

我们将训练集随机分为4个等大小的集合，编号a,b,c,d（此时测试集不进行考虑）会进行四轮训练，

第一轮，以a,b,c为训练集，d为验证集，第二轮，a,b,d为训练集，c为验证集，以此类推，得到四轮训练模型。得到一个平均的结果，更加可信

运用到了基本的信息熵理论

信息熵和消除不确定性是相关的

信息增益：得知一个特征条件后，减少的信息熵的大小

信息增益越大，作为判断依据越优先,具体数学内容不做了解了，看不完了哈哈我靠

网格搜索

用于调参，也称为超参数搜索，有的时候一节参数需要手动设置，比如knn算法中的k值，这种参数称为超参数，手动过于复杂，对模型预设几组参数组合，每组参数采用交叉验证来进行评估，最后选出最优参数建立模型，假设有两个参数属于超参数，则设定两组参数组，使其进行排列组合后得到最优解。

使用api：sklearn.model_selection.GridSearchCV

def knn():
    """
    knn算法预测入驻位置
    :return: None
    """
    #读入数据
    #使用pandas读入csv文件
    data = pd.read_csv('./data/train.csv')
    #进行测试，打印前10条
    # print(data.head(10))
    #处理数据
    #1.缩小数据量，使用pandas中的query
    data=data.query("x > 1.0 & x < 2.0 & y > 1.0 & y < 2.0")
    #2.对时间进行处理，使用pandas中的to_datetime实现,必须有返回值,返回时间格式的数据datetime
    time_value = pd.to_datetime(data['time'], unit='s')
    # print(time_value)
    # 通过对处理过的时间戳数据进行处理，提取出新的特征，构造出新的特征
    #使用datetimeindex进行处理，将时间格式的数据转化为字典格式,可以直接获取年月日等数据
    time_value = pd.DatetimeIndex(time_value)
    # 加入特征
    data['day']=time_value.day
    # data['year']=time_value.year
    data['month']=time_value.month
    data['hour']=time_value.hour
    data['weekday']=time_value.weekday
    #删除时间戳特征，使用drop,删除time,axis=1代表以列删除
    data.drop(['time'],axis=1)
    # print(data)
    #进行筛选，将入住人数少的place_id去掉
    #返回一个以place_id进行groupby后的数据流,输出的place_count后的剩余列会被count的数值所取代，完成了计数的目的
    #所以这里只用place_id和后面的数量进行筛选就好了
    place_count=data.groupby('place_id').count()
    #将少于3人入住的样本去掉，并重设索引，place_count是以place_id为索引
    #tf以通过reset_index()让其以之前的模式以row_id0,1,2,3。。。为索引
    tf=place_count[place_count.row_id>3].reset_index()
    # 对data进行筛选，以place_id为条件
    #使用了DateFrame中布尔索引，可以用满足布尔条件的列值来过滤数据
    data=data[data['place_id'].isin(tf.place_id)]
    #取出数据当中的特征值和目标值
    #设定特征值和目标值
    #特征值x
    x=data.drop(['place_id','row_id'],axis=1)
    #目标值y
    y=data['place_id']


    #数据分割
    x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.25)
    #特征工程,对训练集和测试集的特征值都需要进行，因为
    std=StandardScaler()
    x_train=std.fit_transform(x_train)
    #以已经进行特征预处理后的x_train格式来对x_test进行处理，这样二者格式才相同
    x_test=std.fit_transform(x_test)
    #利用算法进行训练
    #实例化，与k=5，当使用网格搜索时去掉这里的参数
    knn= KNeighborsClassifier()
    params_id={"n_neighbors":[3,5,7,10]}    #多个n_neighbors进行验证
    msgv=GridSearchCV(knn,params_id,cv=3)   #传入三个参数，第一个是估计器，第二个是超参数，第三个是交叉验证划分的个数
    #传入数据
    msgv.fit(x_train,y_train)
    print("预测的准确率：",msgv.score(x_test,y_test))
    print("交叉验证中最好的结果：",msgv.best_score_)
    print("交叉验证中最好的模型：",msgv.best_estimator_)
    print("每次交叉验证后的测试集准确率结果和训练集准确率结果",msgv.cv_results_)
    #传入训练集特征值和目标值
    # knn.fit(x_train,y_train)
    # y_predict=knn.predict(x_test)
    # print("预测的位置",y_predict)
    # print("预测准确率",knn.score(x_test,y_test))
    return None

常用回归算法

回归：目标值是连续值，主要就是找到相关关系

线性回归

线性回归：寻找一种能预测的趋势
线性关系：二维：直线关系，三维：特征，目标值，平面当中

线性关系模型：一个通过属性的线性组合来进行预测的函数

f(x)=w1x1+w2x2+….+wdxd+b

这里的x1，x2…是特征，w1,w2，w3等称为权重，b是偏置顶

需要进行标准化处理，因为当一个特征的值太大时会对结果产生影响

线性回归定义：定义：线性回归通过一个或者多个自变量（）与因变量之间进行建模的回归分析。其中可以为一个或多个自变量之间的的线性组合（线性回归的一种）

一元线性回归：涉及到的变量只有一个
多元线性回归：涉及到的变量两个或两个以上

将权重和特征转化为矩阵做矩阵相乘，

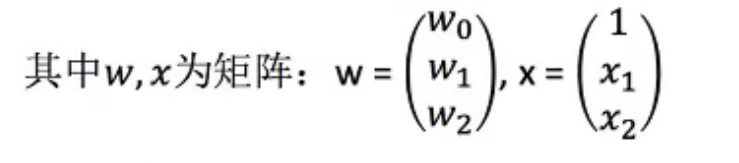
回归以及深度学习的模型算法都是迭代的算法，即一次次的优化更新，逐渐的接近目标值，减少误差

损失函数

最终目的：求解除让误差值最小的w

最小二乘法梯度下降：通过公式，沿着函数下降方向寻找，得到最适合的w值，更新w值（对 w值的循环迭代一般就是用最小二乘法，一般使用梯度下降使用正规方程的一般较少）

线性回归的整个核心思想可以理解为：

使用api：sklearn.linear_model.SGDRegressor

from sklearn.datasets import load_boston    #导入数据集
from sklearn.linear_model import LinearRegression,SGDRegressor  #线性回归api
import pandas as pd
from sklearn.model_selection import train_test_split#数据集分割
from sklearn.preprocessing import StandardScaler#标准化
def ln():
    """
    线性回归预测房价
    :return: none
    """
    data =load_boston()
    #分割数据
    x_train,x_test,y_train,y_test=train_test_split(data.data,data.target,test_size=0.25)
    #标准化
    std_x=StandardScaler()
    std_y=StandardScaler()
    #特征值
    x_train=std_x.fit_transform(x_train)
    x_test=std_x.transform(x_test)
    # print(x_test)
    #目标值
    #这里会出错，因为标准化api要求必须传入二维的参数，这里直接传入Y-train等会有错误，需要进行格式转化，使用reshape
    y_train=std_y.fit_transform(y_train.reshape(-1,1))
    y_test=std_y.transform(y_test.reshape(-1,1))
    # print(y_test)
    #进行预测
    lr =LinearRegression()
    lr.fit(x_train,y_train)
    y_preidict=lr.predict(x_test)
    print("回归系数w：",lr.coef_)
    print("预测价格(没有标准化处理)",y_preidict)
    y_preidict=std_y.inverse_transform(y_preidict)  #将数据转换为原来的样式，这里会转换为房价
    print("预测价格",y_preidict)
    return  None

if __name__=="__main__":
    ln()

深度学习

基于Keras的深度学习，keras的便捷性让我们选择其作为入门深度学习的第一选择**以《python深度学习》作为学习指导**

记录一定的 基础知识：

“深度学习”中的“深度”指 的并不是利用这种方法所获取的更深层次的理解，而是指一系列连续的表示层。数据模型中 包含多少层，这被称为模型的深度，其他机器学习方法的重点往往是仅仅学习一两层的数据表示，因此有时也被称为浅层学习

可以将深度网络看作多级信息蒸馏操作：信息穿过连续的过 滤器，其纯度越来越高（即对任务的帮助越来越大）

• 权重：神经网络对每层所输入的数据所做的具体操作保存在该层的权重中，本质是一串数字，也被称为参数，学习的意思是为神经网络的所有层找到一组 权重值，使得该网络能够将每个示例输入与其目标正确地一一对应，

• 神经网络损失函数：损失函数的输入是网络预测值与真实目标值（即你希望网络输出的 结果），然后计算一个距离值，衡量该网络在这个示例上的效果好坏

• 优化器：利用损失值来对权重值进行一个调整，通过优化器实现了一个迭代的过程，最开始的权重是随机值，随着优化器的不断优化，让损失值不断降低，

这可以看做是深度学习的简要流程

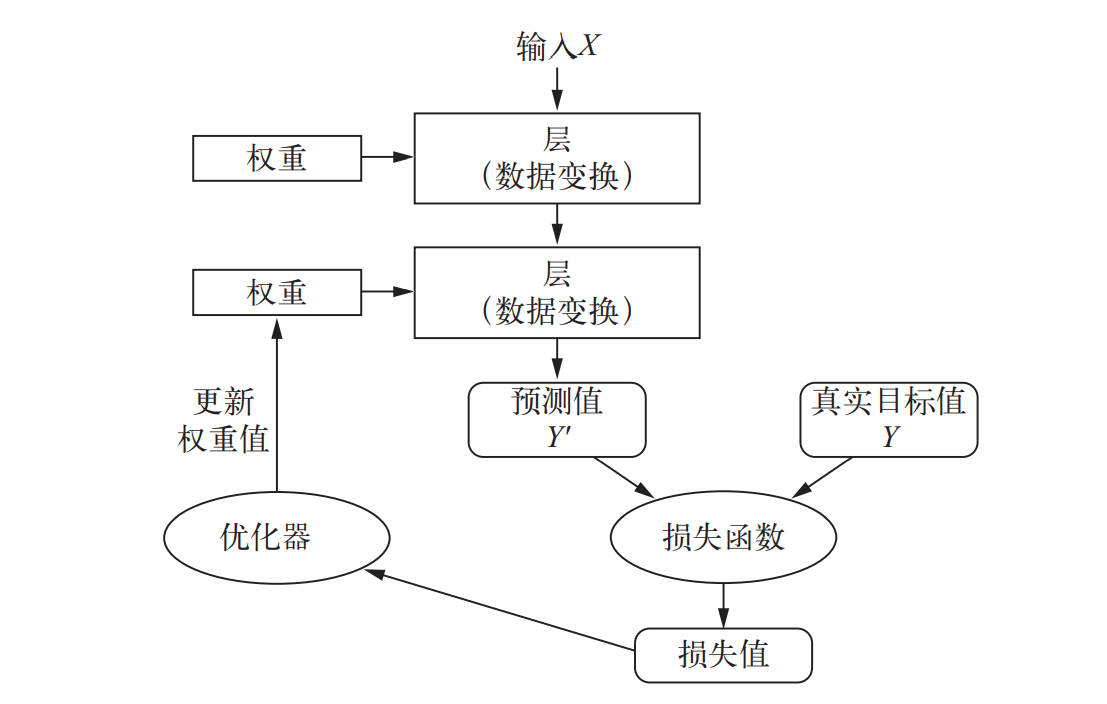
深度学习从数据中进行学习时有两个基本特征：

第一，通过渐进的、逐层的方式形成越来 越复杂的表示；

第二，对中间这些渐进的表示共同进行学习

数据存储在多维 Numpy 数组中，也叫张量（tensor）。一般来说，当前所 有机器学习系统都使用张量作为基本数据结构，张量的维度（dimension）通常叫作轴（axis）

神经网络的数据表示与处理

数据表示

• 标量（0D 张量）：仅包含一个数字的张量叫作标量（scalar，也叫标量张量、零维张量、0D 张量）。在 Numpy 中，一个 float32 或 float64 的数字就是一个标量张量
• 向量（1D 张量）：数字组成的数组叫作向量（vector）或一维张量（1D 张量）。一维张量只有一个轴。
• 矩阵（2D 张量）：向量组成的数组叫作矩阵（matrix）或二维张量（2D 张量）。矩阵有 2 个轴（通常叫作行和 列）。
• 3D 张量与更高维张量将多个矩阵组合成一个新的数组，可以得到一个 3D 张量，你可以将其直观地理解为数字 组成的立方体。
• 关键属性
  • 轴的个数（阶）。例如，3D 张量有 3 个轴，矩阵有 2 个轴。这在 Numpy 等 Python 库中 也叫张量的 ndim可以通过ndim参数查看器轴的个数，也即其维数
  • 形状。这是一个整数元组，表示张量沿每个轴的维度大小（元素个数）。例如，矩阵示例的形状为 (3, 5)，3D 张量示例的形状为 (3, 3, 5)。向量的形状只包含一个 元素，比如 (5,)，而标量的形状为空，即 ()。
  • 数据类型，在 Python 库中通常叫作 dtype，这是张量中所包含数据的类型，例如，张 量的类型可以是 float32、uint8、float64 等。在极少数情况下，你可能会遇到字符 （char）张量。注意，Numpy（以及

除了对这一个张量进行选取，也可以对任意的张量进行选取，比如可以选择后两个张量进行索引截取，

my_slice = train_images[:, 14:, 14:],这表示选取所有样本，取出其右下角14像素x14像素的区域

也可以使用负数索引。与 Python 列表中的负数索引类似，它表示与当前轴终点的相对位置。 你可以在图像中心裁剪出 14 像素×14 像素的区域：my_slice = train_images[:, 7:-7, 7:-7]

• 数据批量：深度学习中所有数据张量的第一个轴（0 轴，因为索引从 0 开始）都是样本轴，深度学习模型不会同时处理整个数据集，而是将数据拆分成小批量，对于这种批量张量，第一个轴（0 轴）叫作批量轴（batch axis）或批量维度

• 将会用到的张量维度：

  • 2D：向量数据，形状为 (samples, features)
    • 这是最常见的数据。对于这种数据集，每个数据点都被编码为一个向量，因此一个数据批 量就被编码为 2D 张量（即向量组成的数组），其中第一个轴是样本轴，第二个轴是特征轴，
    • 例子：人口统计数据集，其中包括每个人的年龄、邮编和收入。每个人可以表示为包含 3 个值 的向量，而整个数据集包含 100 000 个人，因此可以存储在形状为 (100000, 3) 的 2D 张量中。
  • 3D：时间序列数据或序列数据，形状为 (samples, timesteps, features)
    • 当时间（或序列顺序）对于数据很重要时，应该将数据存储在带有时间轴的 3D 张量中。 每个样本可以被编码为一个向量序列（即 2D 张量），因此一个数据批量就被编码为一个 3D 张 量，根据惯例，时间轴始终是第 2 个轴（索引为 1 的轴）
    • 例子： 股票价格数据集。每一分钟，我们将股票的当前价格、前一分钟的最高价格和前一分钟 的最低价格保存下来。因此每分钟被编码为一个 3D 向量，整个交易日被编码为一个形 状为 (390, 3) 的 2D 张量（一个交易日有 390 分钟），而 250 天的数据则可以保存在一 个形状为 (250, 390, 3) 的 3D 张量中。这里每个样本是一天的股票数据
  • 4D：图像，形状为 (samples, height, width, channels) 或 (samples, channels, height, width)
    • 图像通常具有三个维度：高度、宽度和颜色深度(一个像素中，每个颜色分量（Red、Green、Blue、Alpha通道）的比特数)，图像张量始终都是 3D 张量，灰 度图像的彩色通道只有一维。因此，如果图像大小为 256×256，那么 128 张灰度图像组成的批 量可以保存在一个形状为 (128, 256, 256, 1) 的张量中，而 128 张彩色图像组成的批量则可以保存在一个形状为 (128, 256, 256, 3) 的张量中
  • 5D：视频，形状为 (samples, frames, height, width, channels) 或 (samples, frames, channels, height, width)
    • 视频数据是现实生活中需要用到 5D 张量的少数数据类型之一。视频可以看作一系列帧， 每一帧都是一张彩色图像。由于每一帧都可以保存在一个形状为 (height, width, color_ depth) 的 3D 张量中，，因此一系列帧可以保存在一个形状为 (frames, height, width, color_depth) 的 4D 张量中，而不同视频组成的批量则可以保存在一个 5D 张量中，其形状为 (samples, frames, height, width, color_depth)
    • 一个以每秒 4 帧采样的 60 秒 YouTube 视频片段，视频尺寸为 144×256，这个 视频共有 240 帧。4 个这样的视频片段组成的批量将保存在形状为 (4, 240, 144, 256, 3) 的张量中。

• 大多数其他库）中不存在字符串张量

数据处理

深度神经网络学到的所有变换也都可以简化为数值数据张量上的一些张量运算，例如relu(x) 是 max(x, 0)

• 逐元素运算：relu 运算和加法都是逐元素（element-wise）的运算，即该运算独立地应用于张量中的每 个元素，通过numpy可以高效的实现一些逐元素运算，，例如：

• 广播：上述例子中逐元素运算中值适合于两个形状相同的张量相加，如果将两个形状不同的张量相加，如果没有歧义的话，较小的张量会被广播，以匹配较大张量的形状，广播包含以下两步：

  • 向较小的张量添加轴（叫作广播轴），使其 ndim 与较大的张量相同
  • 将较小的张量沿着新轴重复，使其形状与较大的张量相同
  • 一个具体的例子。假设 X 的形状是 (32, 10)，y 的形状是 (10,)。首先，我们给 y 添加空的第一个轴，这样 y 的形状变为 (1, 10)。然后，我们将 y 沿着新轴重复 32 次，这样 得到的张量 Y 的形状为 (32, 10)，并且 Y[i, :] == y for i in range(0, 32)。现在， 我们可以将 X 和 Y 相加，因为它们的形状相同。
  • 下面这个例子利用广播将逐元素的 maximum 运算应用于两个形状不同的张量，这样就可以完成2D张量y的广播

  

• 张量点积：点积运算，也叫张量积，不是逐元素的相乘，是最常见也最有用的 张量运算。与逐元素的运算不同，它将输入张量的元素合并在一起

  • 在 Numpy、Keras、Theano 和 TensorFlow 中，都是用 * 实现逐元素乘积。TensorFlow 中的 点积使用了不同的语法，但在 Numpy 和 Keras 中，都是用标准的 dot 运算符来实现点积,

  

  • 点积运算做了以下工作：注意，两个向量之间的点积是一个标量，而且只有元素个数相同的向量之间才能做点积。

  

  • 你还可以对一个矩阵 x 和一个向量 y 做点积，返回值是一个向量，其中每个元素是 y 和 x 的每一行之间的点积。其实现过程如下。

  

  • 注意，如果两个张量中有一个的 ndim 大于 1，那么 dot 运算就不再是对称的，也就是说， dot(x, y) 不等于 dot(y, x)
  • 当然，点积可以推广到具有任意个轴的张量。最常见的应用可能就是两个矩阵之间的点积。 对于两个矩阵 x 和 y，当且仅当 x.shape[1] == y.shape[0] 时，你才可以对它们做点积 （dot(x, y)）。得到的结果是一个形状为 (x.shape[0], y.shape[1]) 的矩阵，其元素为 x 的行与 y 的列之间的点积。如果对于2D张量其实就是矩阵相乘。。。

• 张量变形：张量变形是指改变张量的行和列，以得到想要的形状。变形后的张量的元素总个数与初始 张量相同。

  

  • 经常遇到的一种特殊的张量变形是转置（transposition）。对矩阵做转置是指将行和列互换， 使 x[i, :] 变为 x[:, i]。

###　神经网络的梯度优化：

神经网络都是依靠梯度进行优化的，对于一个例子：output = relu(dot(W, input) + b):

在这个表达式中，W 和 b 都是张量，均为该层的属性。它们被称为该层的权重或可训练参数，这些权重包含网络从观察 训练数据中学到的信息，一开始，这些权重矩阵取较小的随机值，这一步叫作随机初始化，W 和 b 都是随机的，relu(dot(W, input) + b) 肯定不会得到任何有用的表示。虽然 得到的表示是没有意义的，但这是一个起点。下一步则是根据反馈信号逐渐调节这些权重。这 个逐渐调节的过程叫作训练，也就是机器学习中的学习

上述过程发生在一个训练循环（training loop）内，其具体过程如下。必要时一直重复这些 步骤。

1. 抽取训练样本 x 和对应目标 y 组成的数据批量
2. 在 x 上运行网络［这一步叫作前向传播（forward pass）］，得到预测值 y_pred。
3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离。
4. 更新网络的所有权重，使网络在这批数据上的损失略微下降。

最终得到的网络在训练数据上的损失非常小，即预测值 y_pred 和预期目标 y 之间的距离 非常小。网络“学会”将输入映射到正确的目标。

难点在于：更新网 络的权重。考虑网络中某个权重系数，你怎么知道这个系数应该增大还是减小，以及变化多少

现在普遍使用的方法就是：计算损失相对于网络系数的梯度（gradient），然后向梯度 的反方向改变系数，从而使损失降低

这里对梯度做一个回顾，是微积分中的内容：梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

简单来说，通过梯度，可以找到函数最快的下降方向，这样对于权重的更新是高效的方法，当然，这里以二元函数为例，但在深度学习中的权重会很多，函数的维度会很高，但原理是相同的。

具体步骤如下：

1. 抽取训练样本 x 和对应目标 y 组成的数据批量
2. 在 x 上运行网络，得到预测值 y_pred。
3. 计算网络在这批数据上的损失，用于衡量 y_pred 和 y 之间的距离。
4. 计算损失相对于网络参数的梯度［一次反向传播（backward pass）］。
5. 将参数沿着梯度的反方向移动一点，比如 W -= step * gradient，从而使这批数据 上的损失减小一点。

上述方法叫做小批量随机梯度下降（SGD），注意，小批量 SGD 算法的一个变体是每次迭代时只抽取一个样本和目标，而不是抽取一批 数据。还有另一种极端，每一次迭代都在所有数据上 运行，这样做的话，每次更新都更加准确，但计算代价也高得多。这两个极 端之间的有效折中则是选择合理的批量大小。

此外，SGD 还有多种变体，其区别在于计算下一次权重更新时还要考虑上一次权重更新， 而不是仅仅考虑当前梯度值，比如带动量的 SGD、Adagrad、RMSProp 等变体。这些变体被称 为优化方法（optimization method）或优化器（optimizer）。因为SGD会有缺陷，比如：

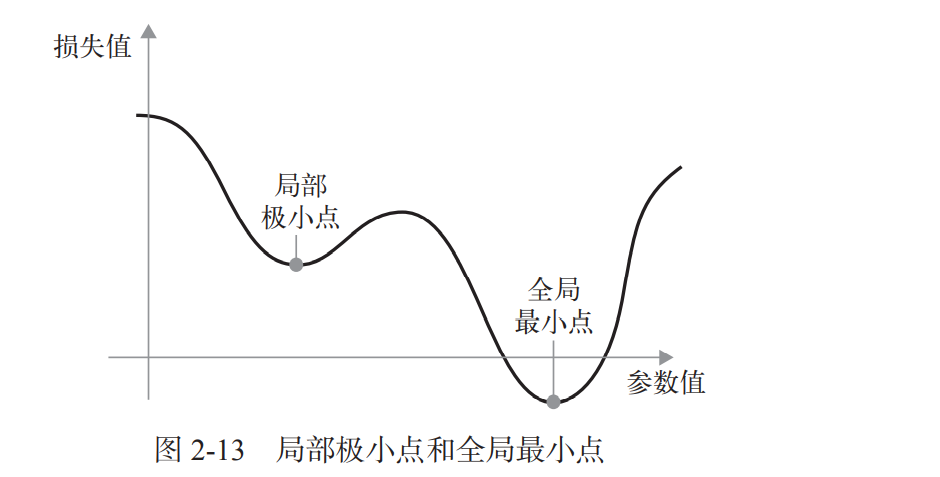
在某个参数值附近，有一个局部极小点，在这个点附近，向 左移动和向右移动都会导致损失值增大。如果使用小学习率的 SGD 进行优化，那么优化过程可 能会陷入局部极小点，导致无法找到全局最小点。所以动量的概念尤其值得关注，它在 许多变体中都有应用。动量解决了 SGD 的两个问题：收敛速度和局部极小点。这在实践中的是指， 更新参数 w 不仅要考虑当前的梯度值，还要考虑上一次的参数更新，具体示例如下：

链式求导：反向传播算法

在前面的算法中，我们假设函数是可微的，因此可以明确计算其导数。在实践中，神经网 络函数包含许多连接在一起的张量运算，每个运算都有简单的、已知的导数。例如，下面这个 网络 f 包含 3 个张量运算 a、b 和 c，还有 3 个权重矩阵 W1、W2 和 W3。 f(W1, W2, W3) = a(W1, b(W2, c(W3)))

根据微积分的知识，这种函数链可以利用下面这个恒等式进行求导，它称为链式法则（chain rule）：(f(g(x)))’ = f’(g(x)) * g’(x)。将链式法则应用于神经网络梯度值的计算，得 到的算法叫作反向传播（backpropagation，有时也叫反式微分，

回顾本章的第一个例子，已经可以简要明白整个神经网络的训练过程：

到这里前置知识就算是结束了，自己感觉对于神经网络最精简的理解还是这个图，上述的所有内容都可以归入这个图里，也算是对专业术语的一个了解了，终于可以开始了写代码了，淦：

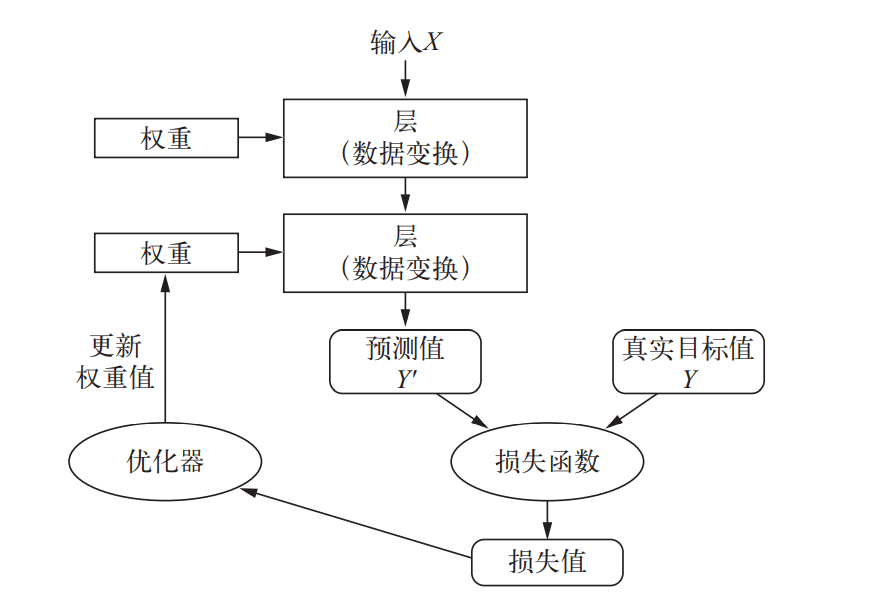
神经网络入门

针对上图，将要对层，输入数据，损失函数，优化器进行理解记录，这样就能简要完整实现一个神经网络模型

神经网络结构：

层

层，是神经网络的基本数据结构。层是一个数据处理模块，将一个 或多个输入张量转换为一个或多个输出张量。有些层是无状态的，但大多数的层是有状态的， 即层的权重。权重是利用随机梯度下降学到的一个或多个张量，其中包含网络的知识

• 对于2D模型：形状为 (samples, features)，通常用密集连接层，也 叫全连接层或密集层，对应于 Keras 的 Dense 类，来进行处理

• 对于3D模型：形状为 (samples, timesteps, features)，通常用循环 层（recurrent layer，比如 Keras 的 LSTM 层）来进行处理

• 对于4D模型：通常用二维 卷积层（Keras 的 Conv2D）来处理

在 Keras 中，构 建深度学习模型就是将相互兼容的多个层拼接在一起，以建立有用的数据变换流程

这里层兼 容性（layer compatibility）具体指的是每一层只接受特定形状的输入张量，并返回特定形状的输 出张量。看看下面这个例子

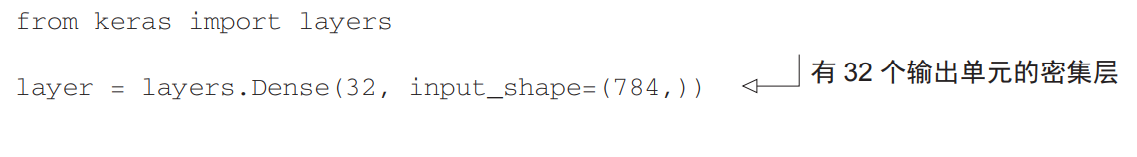
我们创建了一个层，只接受第一个维度大小为 784 的 2D 张量（第 0 轴是批量维度，其大 小没有指定，因此可以任意取值）作为输入。这个层将返回一个张量，第一个维度的大小变成 了 32。因此，这个层后面只能连接一个接受 32 维向量作为输入的层。在Keras中，不用担心，因为向模型中添加的层都会自动匹配输入层的形状，

模型

深度学习模型是层构成的有向无环图。最常见的例子就是层的线性堆叠，将单一输入映射 为单一输出。但这并不是唯一的结构，会有更多的网络拓扑结构：

双支头网络，多头网络， Inception 模块，等，选择合适的拓扑结构是很重要的，后续会学到如何选择

损失函数与优化器

一旦确定了网络架构，就需要选择损失函数与优化器两个参数，

• 损失函数（目标函数）——在训练过程中需要将其最小化。它能够衡量当前任务是否已 成功完成。
• 优化器——决定如何基于损失函数对网络进行更新。它执行的是随机梯度下降（SGD） 的某个变体。

具有多个输出的神经网络可能具有多个损失函数（每个输出对应一个损失函数）。但是，梯度下降过程必须基于单个标量损失值。因此，对于具有多个损失函数的网络，需要将所有损失 函数取平均，变为一个标量值

二分类问题

使用Keras中的数据集 IMDB,本节使用 IMDB 数据集，它包含来自互联网电影数据库（IMDB）的 50 000 条严重两极分 化的评论。数据集被分为用于训练的 25 000 条评论与用于测试的 25 000 条评论，训练集和测试 集都包含 50% 的正面评论和 50% 的负面评论,它已经过预处理：评论（单词序列） 已经被转换为整数序列，其中每个整数代表字典中的某个单词

不能将整数序列直接传入神经网络，需要将列表转化为张量，

• 可以填充列表使其具有相同的长度，再将列表转换成形状为 (samples, word_indices) 的整数张量，然后网络第一层使用能处理这种整数张量的层
• 对列表进行 one-hot 编码，将其转换为 0 和 1 组成的向量。举个例子，序列 [3, 5] 将会 被转换为 10 000 维向量，只有索引为 3 和 5 的元素是 1，其余元素都是 0。然后网络第 一层可以用 Dense 层，它能够处理浮点数向量数据。

输入数据是向量，而标签是标量（1 和 0），

带有 relu 激活的全连接层（Dense）的简单堆叠在这种问题上表现的很好，，比如 Dense(16, activation=’relu’)

传入 Dense 层的参数（16）是该层隐藏单元的个数。一个隐藏单元（hidden unit）是该层 表示空间的一个维度。

relu叫做激活函数

最后需要选择损失函数和优化器

面对二分类问题，网络输出是一个概率值，网络最后一层使用 sigmoid 激活函数，仅包含一个单元），那么最好使用 binary_ crossentropy（二元交叉熵）损失。这并不是唯一可行的选择，比如你还可以使用 mean_ squared_error（均方误差）。但对于输出概率值的模型，交叉熵（crossentropy）往往是最好 的选择。交叉熵是来自于信息论领域的概念，用于衡量概率分布之间的距离，在这个例子中就 是真实分布与预测值之间的距离

为了在训练过程中监控模型在前所未见的数据上的精度，需要将原始训练数据留出 10000 个样本作为验证集。

验证集的作用是用于辅助调剂模型，在跑了一定的轮次后可以通过验证集来确定当前参数是否是优解，如果在验证集上的效果比训练集上差很多，考虑模型是否过拟合了。同时，还可以通过验证集对比不同的模型。

以下代码为例：

from keras.datasets import imdb    #导入数据集
import numpy as np
from keras import models    #模型
from keras import layers    #层
def div():
    """
    利用简单神经网络实现二分类
    :return:
    """
    #读取数据，num_words=10000意思是仅保留训练数据中前 10 000 个最常出现的单词
    #train_data是训练集特征，train_lables是训练集目标值，test_data是测试集特征值，test_labels是测试机目标值
    #都是还未经过处理的，也可以直接以x_train等代替
    (train_data,train_labels),(test_data,test_labels)= imdb.load_data(num_words=10000)
    #print可以看到train_data的类型是列表，不能直接传入神经网络模型，需要进行格式转化
    x_train=vectorize_sequences(train_data)
    x_test=vectorize_sequences(test_data)
    y_train = np.asarray(train_labels).astype('float32')
    y_test = np.asarray(test_labels).astype('float32')
    #模型实例化
    model = models.Sequential()
    #给模型添加层
    model.add(layers.Dense(16,activation='relu',input_shape=(10000,)))
    model.add(layers.Dense(16,activation='relu'))
    model.add(layers.Dense(1,activation='sigmoid'))
    #模型编译，将优化器、损失函数和指标的设置
    model.compile(optimizer='rmsprop',loss='binary_crossentropy',metrics=['accuracy'])
    #进行验证集划分，x_val为训练集特征值的训练集划分
    x_val = x_train[:10000]
    #剩余训练集特征值
    prac_x_train=x_train[10000:]
    #目标值也进行划分
    y_val = y_train[:10000]
    prac_y_train = y_train[10000:]
    #传入数据进行迭代训练
    #第一个参数为训练集特诊值，第二个为训练集目标值，第三个参数epochs为训练轮数，batch_size为批量中样本个数，validation_data为验证集
    predict=model.fit(prac_x_train,prac_y_train,epochs=20,batch_size=512,validation_data=(x_val,y_val))
       #进行预测,用于评估模型性能
    #返回损失值和你选定的指标值（例如，精度accuracy
    result=model.evaluate(x_test,y_test)
    print(result)



def vectorize_sequences(sequence,dimention=10000):

    """
    向量化数据,做了一个转化数据格式的作用
    :param sequence:传入数据
    :param dimention:数量
    :return:
    """
    #创建一个大小为(sequence,dimention)的0矩阵
    result= np.zeros((len(sequence),dimention))
    for i,se in enumerate(sequence):
        result[i,se]=1
    return result


if __name__=='__main__':
    div()

运行后可得20个轮次的结果

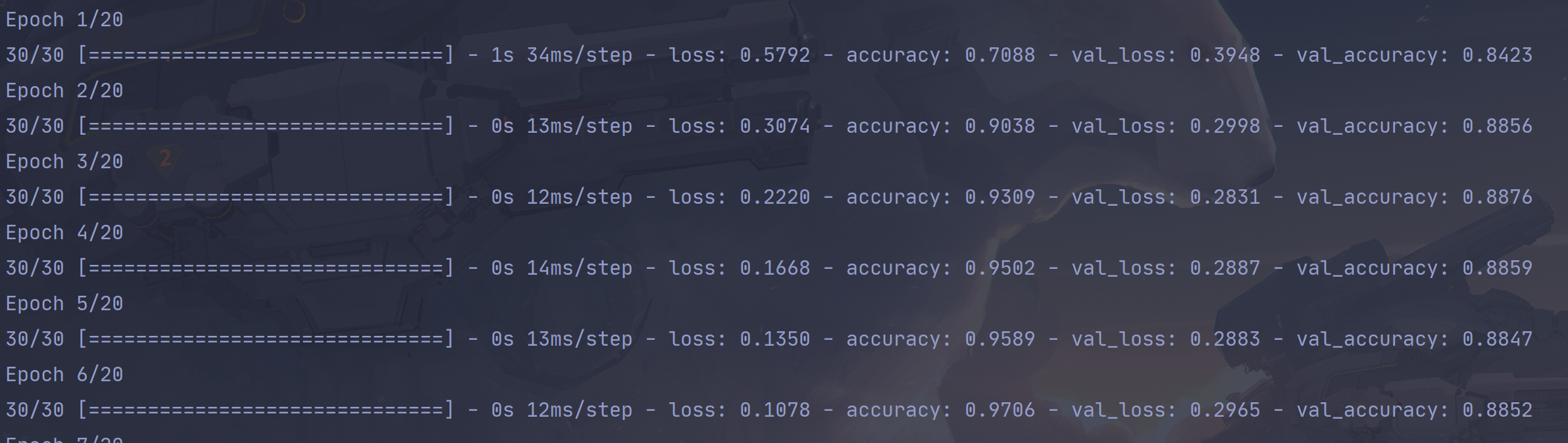
• loss：是网络在训练数据上的损失（loss），

• accuracy：是网络在 训练数据上的精度（acc）

• val_loss:验证集的数据损失

• val_accuracy:验证集的精度

多分类问题

也是分类问题，但目标值有多个，属于多分类问题，每个数据点只能划分到一个类别， 所以更具体地说，这是单标签、多分类，如果每个数据点可以划分到多个类别（主题），那它就是一个多标签、多分类问题

在对数据做处理时，对这次的数据集，路透社数据集，与 IMDB 评论一样，每个样本都是一个整数列表（表示单词索引）

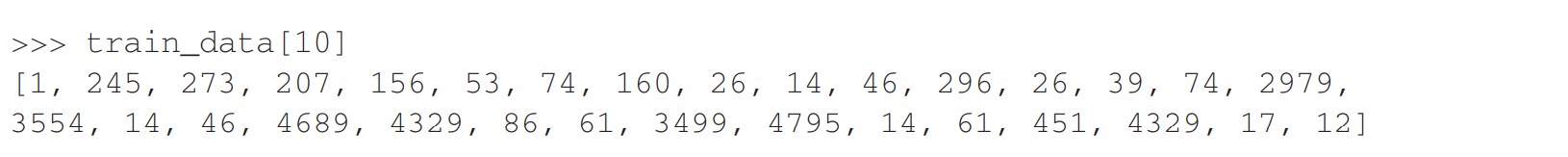
这种需要对其使用one_hot编码或者像上一个例子中一样进行转化，，这里直接使用keras中的api对特征值和目标值进行转化：api：

from keras.utils.np_utils.to_categorical

完成数据转换后就按照之前的步骤模型定义和搭建神经网络即可，

def div_mul():
    """
    多分类神经网络
    :return:
    """
    #导入数据
    (train_data,train_labels),(test_data,test_labels)=reuters.load_data(num_words=10000)
    # print(train_data[0])
    # print(test_labels)
    #数据处理，转化为one_hot编码,直接调用api
    """
    这里直接对train_data,test_data调用api会有错误，
    因为x_train的格式是类似arry([[list([12.0, 25.0,]), list([20.0, 21.0,])])
    这种，不是np.array的形式，需要转化为这种形式才能进行
    试验后发现，train_data中每个元素的长度不同，不能直接调api，只能用自己写的10000长度的to one hot 
    """
    # x_train = np.array([data for data in train_data])
    # x_train=to_categorical(x_train.astype('float32'))
    # x_test=np.array([data for data in test_data])
    # x_test=to_categorical(x_test.astype('float32'))
    x_train = vectorize_sequences(train_data)
    x_test = vectorize_sequences(test_data)
    y_train=to_categorical(train_labels,)
    y_test=to_categorical(test_labels,)
    #模型定义,大小64,46的Dense层
    #网络的最后一层是大小为 46 的 Dense 层。这意味着，对于每个输入样本，网络都会输出一个 46 维向量。这个向量的每个元素（即每个维度）代表不同的输出类别
    #  最后一层使用了 softmax 激活。,网络将输出在 46个不同输出类别上的概率分布——对于每一个输入样本，网络都会输出一个 46 维向量，
    # 其中 output[i] 是样本属于第 i 个类别的概率。46 个概率的总和为 1
    model=models.Sequential()
    model.add(layers.Dense(64,activation='relu',input_shape=(10000,)))
    model.add(layers.Dense(64,activation='relu'))
    model.add(layers.Dense(46,activation='softmax'))
    #对于这个例子，最好的损失函数是 categorical_crossentropy（分类交叉熵）。它用于
    #衡量两个概率分布之间的距离，这里两个概率分布分别是网络输出的概率分布和标签的真实分
    #布。通过将这两个分布的距离最小化，训练网络可使输出结果尽可能接近真实标签。
    #编译模型
    model.compile(optimizer='rmsprop',loss='categorical_crossentropy',metrics=['accuracy'])
    #验证集划分
    x_val_train = x_train[:1000]
    x_train = x_train[1000:]
    y_val_train = y_train[:1000]
    y_train = y_train[1000:]
    #传入训练数据
    result=model.fit(x_train,y_train,epochs=20,batch_size=512,validation_data=(x_val_train,y_val_train))
    print("测试集预测结果",model.evaluate(x_test,y_test))

对于3个Dense层，其大小都是64或46，是大于等于目标值，标签值的46的。因为最终输出是 46 维的，因此中间层的隐藏单元个数不应该比 46 小太多，如果中间层的维度小于46，，就会造成信息瓶颈，降低准确值

原因：试图将大量信息（这些信息足够恢复 46 个类别的分割超平面）压缩到维度很小的中间空间。网 络能够将大部分必要信息塞入这个四维表示中，但并不是全部信息

回归问题

上述两个例子都是分类问题，在之前的机器学习中也通过knn，朴素贝叶斯，决策树随机森林进行了分类，回归问题也是机器学习中重要的问题之一，分类问题的数据使用的离散型，而回归问题的数据是连续型，

对这个数据，我们需要进行标准化处理，可以调用api，也可以自己写一下，

对于回归问题的模型构建，其优化器一般使用rmsprop,而损失函数一般使用是mse 损失函数，即均方误差，预测值与 目标值之差的平方。这是回归问题常用的损失函数，监控指标为平均绝对误差，MAE，它是预测值 与目标值之差的绝对值。、

对于数据集较少的情况，验证集的划分需要用到交叉验证，之前有过记录

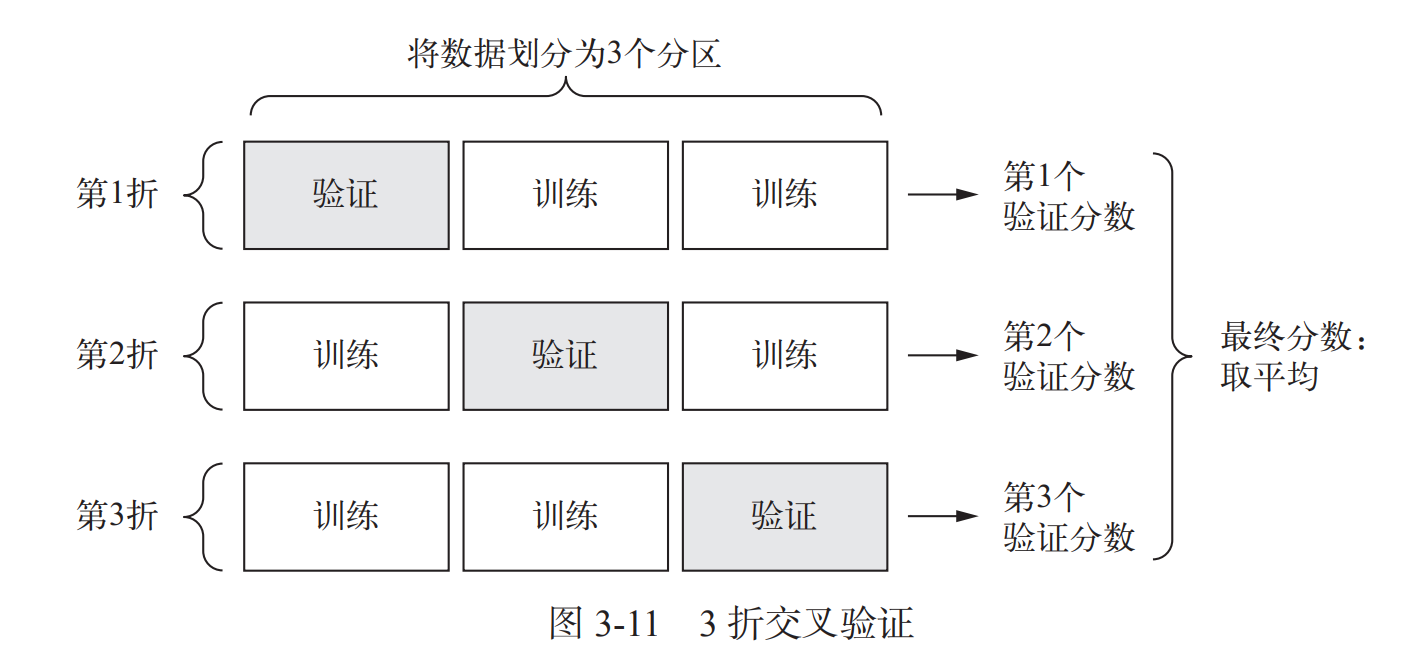
通过交叉验证来查看mae等参数，进行调参，最后得到合适的参数，再在所有的数据集上训练，最后通过训练除的模型来进行预测

def regress():
    """
    回归问题,波士顿房价
    :return:None
    """
    #读入数据
    (x_train,y_train),(x_test,y_test)=boston_housing.load_data()
    #需要对数据进行标准化，可以调用sklearn的api，也可以自己写一个
    # 平均数
    mean = x_train.mean(axis=0)
    #标准差i
    std = x_train.std(axis=0)
    x_train -=mean
    x_train /=std
    x_test-=mean
    x_test /=std
    #因为要多次实例化同一个模型，所以将模型定义放入函数def_model中
    #手动实现k折交叉验证
    k=3
    #验证集长度
    num_of_val = len(x_train)//k
    #训练轮次
    num_epochs = 80
    #训练结果
    all_score=[]
    for i in range(k):
        #进行k折交叉验证
        print(i,"折")
        #验证集特征值
        val_x = x_train[i*num_of_val:(i+1)*num_of_val]
        #验证集目标值
        val_y = y_train[i*num_of_val:(i+1)*num_of_val]
        #数据集,用np将其聚合起来
        val_x_train = np.concatenate(
            [x_train[:i*num_of_val],x_train[(i+1)*num_of_val:]]
            ,axis=0
        )
        val_y_train = np.concatenate(
            [y_train[:i*num_of_val],y_train[(i+1)*num_of_val:]]
            ,axis=0
        )
        model = def_model()
        # 模型训练
        history = model.fit(val_x_train,val_y_train,validation_data=(val_x,val_y),epochs=num_epochs,batch_size=1)
        #在验证集上进行预测
        mse,mae = model.evaluate(val_x,val_y)
        print(mae)
        #最终通过k折交叉验证找到合适的参数，在全部训练集上进行训练，得到最终模型，进行预测
        model1=def_model()
        model1.fit(x_train,y_train,epochs=80,batch_size=16)
        fin_mse,fin_mae=model1.evaluate(x_test,y_test)


def def_model():
    """
    回归模型构建
    :return: model
    """
    #实例化对象
    model = models.Sequential()
    # 现在模型就会以尺寸为 (*, 13) 的数组作为输入，
    # 其输出数组的尺寸为 (*, 64)
    model.add(layers.Dense(64,activation='relu',input_shape=(13,)))
    model.add(layers.Dense(64,activation='relu'))
    #网络的最后一层只有一个单元，没有激活，是一个线性层。这是标量回归（标量回归是预测单一连续值的回归）的典型设置
    # 添加激活函数将会限制输出范围,这里最后一层是纯线性的，所以网络可以学会预测任意范围内的值
    model.add(layers.Dense(1))
    #损失函数mse，即均方误差，预测值与
    # 目标值之差的平方。这是回归问题常用的损失函数
    # 在训练过程中还监控一个新指标：平均绝对误差，它是预测值与目标值之差的绝对值
    model.compile(optimizer='rmsprop',loss='mse',metrics=['mae'])
    return model


if __name__=='__main__':
    regress()

回归问题使用的损失函数与分类问题不同。回归常用的损失函数是均方误差（MSE），同样，回归问题使用的评估指标也与分类问题不同。显而易见，精度的概念不适用于回 归问题。常见的回归指标是平均绝对误差（MAE）。

如果输入数据的特征具有不同的取值范围，应该先进行预处理，对每个特征单独进行 缩放，进行标准化处理，如果可用的数据很少，使用 K 折交叉验证可以可靠地评估模型。

如果可用的训练数据很少，最好使用隐藏层较少（通常只有一到两个）的小型网络，以 避免严重的过拟合。

到目前，机器学习中的分类以及回归问题都以神经网络的方式进行了实现，对其进行一个简要的总结

• 在将原始数据输入神经网络之前，通常需要对其进行预处理。

• 如果数据特征具有不同的取值范围，那么需要进行预处理，将每个特征单独缩放。

• 随着训练的进行，神经网络最终会过拟合，并在前所未见的数据上得到更差的结果。

• 如果训练数据不是很多，应该使用只有一两个隐藏层的小型网络，以避免严重的过拟合。

• 如果数据被分为多个类别，那么中间层过小可能会导致信息瓶颈。

• 回归问题使用的损失函数和评估指标都与分类问题不同。

• 如果要处理的数据很少，K 折验证有助于可靠地评估模型

深度学习数据预处理

之前对于机器学习的处理中，已经了解到了数据处理，特征工程的重要性，对于模型的准确率是很重要的，同样的，在深度学习中，对数据的预处理会对神经模型的准确率有很大的影响。

神经网络的数据预处理

数据预处理的目的是使原始数据更适于用神经网络处理，包括向量化、标准化、处理缺失 值和特征提取

1. 向量化：神经网络的所有输入和目标都必须是浮点数张量（在特定情况下可以是整数张量）。无论 处理什么数据（声音、图像还是文本），都必须首先将其转换为张量，这一步叫作数据向量化，例如，在前面两个文本分类的例子中，开始时文本都表示为整数列表（代 表单词序列），用 one-hot 编码将其转换为 float32 格式的张量。在手写数字分类和预 测房价的例子中，数据已经是向量形式，所以可以跳过这一步
2. 值标准化，就是特征的标准化，对每个特征分别做标准化，使 其均值为 0、标准差为 1。一般来说，将取值相对较大的数据（比如多位整数，比网络权重的初始值大很多）或异质 数据（heterogeneous data，比如数据的一个特征在 01 范围内，另一个特征在 100200 范围内） 输入到神经网络中是不安全的。输入数据应该具有以下特征：
   1. 取值较小：大部分值都应该在 0~1 范围内。
   2. 同质性：所有特征的取值都应该在大致相同的范围内，
   3. 简单来说就是标准化，可以直接使用numpy数组完成：x -= x.mean(axis=0) x /= x.std(axis=0
3. 处理缺失值，一般来说，对于神经网络，将缺失值设置为 0 是安全的，只要 0 不是一个有意义的值。网 络能够从数据中学到 0 意味着缺失数据，并且会忽略这个值，如果测试数据中可能有缺失值，而网络是在没有缺失值的数据上训练的，那么网络 不可能学会忽略缺失值。在这种情况下，你应该人为生成一些有缺失项的训练样本：多次复制 一些训练样本，然后删除测试数据中可能缺失的某些特征
4. 特征工程：是指将数据输入模型之前，利用你自己关于数据和机器学 习算法（这里指神经网络）的知识对数据进行硬编码的变换（不是模型学到的），以改善模型的 效果。多数情况下，一个机器学习模型无法从完全任意的数据中进行学习。呈现给模型的数据 应该便于模型进行学习

幸运的是，对于现代深度学习，大部分特征工程都是不需要的，因为神经网络能够从原始 数据中自动提取有用的特征，但并不意味着特征工程就不再使用，良好的特征可以让你用更少的数据解决问题。深度学习模型自主学习特征的能力依赖于 大量的训练数据。如果只有很少的样本，那么特征的信息价值就变得非常重要。

过拟合和欠拟合

模型在留出验证数据上的性能总是在几轮后达到最高点，然后开始下降。也就是说，模型很快就在训练数据上开始过拟合。过拟合存在于所有机器学习问题中。学会如何处理过拟合对掌握机器学习至关重要

机器学习的根本问题是优化和泛化之间的对立，优化是指调节模型以在训 练数据上得到最佳性能（即机器学习中的学习），而泛化是指训练好的模型在 前所未见的数据上的性能好坏。

训练开始时，优化和泛化是相关的：训练数据上的损失越小，测试数据上的损失也越小。 这时的模型是欠拟合，即仍有改进的空间，网络还没有对训练数据中所有相关模 式建模。但在训练数据上迭代一定次数之后，泛化不再提高，验证指标先是不变，然后开始变差， 即模型开始过拟合。这时模型开始学习仅和训练数据有关的模式，但这种模式对新数据来说是 错误的或无关紧要的，为了防止模型从训练数据中学到错误或无关紧要的模式，最优解决方法是获取更多的训练 数据。次优解决方法是调节模型允许存储的信息量，或对模型允许存储的信息加以约束。如果一个网络只能记住几个 模式，那么优化过程会迫使模型集中学习最重要的模式，这样更可能得到良好的泛化。这种降低过拟合的方法叫作正则化

减小网络大小

防止过拟合的最简单的方法就是减小模型大小，即减少模型中可学习参数的个数，在深度学习中，模型中可学习参数的个数通常被称为模型的容量，深度学习模型通常都很擅长拟合训练数据，但真正的挑战在于泛化，而不是拟合，

使用的模型应 该具有足够多的参数，以防欠拟合，即模型应避免记忆资源不足。在容 量过大与容量不足之间要找到一个折中。

一般的工作流程是开始时选择相对较少的层和参数，然后逐渐增加层，的大小或增加新层，直到这种增加对验证损失的影响变得很小。

添加权重正则化

给 定一些训练数据和一种网络架构，很多组权重值（即很多模型）都可以解释这些数据。简单模 型比复杂模型更不容易过拟合。

这里的简单模型是指参数值分布的熵更小的模型（或参数更少的模型，一种常见的降低过拟合的方法就是强制让模型权重只能取较小的值， 从而限制模型的复杂度，这使得权重值的分布更加规则，这种方法叫作权重正则化，其实现方法是向网络损失函数中添加与较大权重值相关的成本：

• L1 正则化：添加的成本与权重系数的绝对值［权重的 L1 范数］ 成正比。
• L2 正则化：添加的成本与权重系数的平方（权重的 L2 范数）成正比。 神经网络的 L2 正则化也叫权重衰减（weight decay）。不要被不同的名称搞混，权重衰减 与 L2 正则化在数学上是完全相同的。、

在 Keras 中，添加权重正则化的方法是向层传递权重正则化项实例，作为关键字参数

from keras import regularizers
model = models.Sequential()
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
 activation='relu', input_shape=(10000,)))
model.add(layers.Dense(16, kernel_regularizer=regularizers.l2(0.001),
 activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

l2(0.001) 的意思是该层权重矩阵的每个系数都会使网络总损失增加 0.001 * weight_ coefficient_value。注意，由于这个惩罚项只在训练时添加，所以这个网络的训练损失会 比测试损失大很多

还可以用 Keras 中以下这些权重正则化项来代替 L2 正则化:

from keras import regularizers
regularizers.l1(0.001) 
regularizers.l1_l2(l1=0.001, l2=0.001)

添加 dropout 正则化

dropout 是神经网络最有效也最常用的正则化方法之一，对某一层使用 dropout，就是在训练过程中随机将该层的一些输出特征舍 弃（设置为 0）。dropout 比率（dropout rate）是被设为 0 的特征所占的比例，通常在 0.2~0.5 范围内。测试时没有单元被舍弃，而该层的输出值需要按 dropout 比率缩小，因为这时比训练时 有更多的单元被激活，需要加以平衡

总结一下，防止神经网络过拟合的常用方法包括：

• 获取更多的训练数据

• 减小网络容量

• 添加权重正则化

• 添加 dropout

这是向神经网络中添加dropout层的示例

model = models.Sequential()
model.add(layers.Dense(16, activation='relu', input_shape=(10000,)))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(16, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))

机器学习通用流程

1. 定义问题，收集数据，只有明确了输入、输出以及所使用的数据，你才能进入下一阶段。注意在这一阶段所做 的假设，假设输出是可以根据输入进行预测的。假设可用数据包含足够多的信息，足以学习输入和输出之间的关系。在开发出工作模型之前，这些只是假设，等待验证真假。并非所有问题都可以解决。你收 集了包含输入 X 和目标 Y 的很多样例，并不意味着 X 包含足够多的信息来预测 Y。

2. 选择衡量成功的指标，衡量成功的指标将指引你选择损失函数，即 模型要优化什么。它应该直接与你的目标（如业务成功）保持一致。

3. 确定评估方法，一旦明确了目标，你必须确定如何衡量当前的进展。前面介绍了三种常见的评估方法

   1. 留出验证集。数据量很大时可以采用这种方法
   2. K 折交叉验证。如果留出验证的样本量太少，无法保证可靠性，那么应该选择这种方法
   3. 重复的 K 折验证。如果可用的数据很少，同时模型评估又需要非常准确，那么应该使用 这种方法。
   4. 只需选择三者之一。大多数情况下，第一种方法足以满足要求

4. 准备数据，首先你应该将数据格式化，使其可以输入到机器学习模型中（这里假设模型为深度神经网络）

   1. 如前所述，应该将数据格式化为张量
   2. 这些张量的取值通常应该缩放为较小的值，比如在 [-1, 1] 区间或 [0, 1] 区间。
   3. 如果不同的特征具有不同的取值范围（异质数据），那么应该做数据标准化
   4. 可能需要做特征工程，尤其是对于小数据问题

5. 开发比基准更好的模型，这一阶段的目标是获得统计功效（statistical power），即开发一个小型模型，它能够打败纯 随机的基准，不一定总是能获得统计功效。如果你尝试了多种合理架构之后仍然无法打败随机基准， 那么原因可能是问题的答案并不在输入数据中，要记住所做的两个假设：

   1. 假设输出是可以根据输入进行预测的。
   2. 假设可用的数据包含足够多的信息，足以学习输入和输出之间的关系
   3. 还需要选择三个关键参数来构建第一个工作模型
      1. 最后一层的激活。它对网络输出进行有效的限制。例如，IMDB 分类的例子在最后一层 使用了 sigmoid，回归的例子在最后一层没有使用激活，等等
      2. 损失函数。它应该匹配你要解决的问题的类型。例如，IMDB 的例子使用 binary_ crossentropy、回归的例子使用 mse，等等
      3. 优化配置。你要使用哪种优化器？学习率是多少？大多数情况下，使用 rmsprop 及其 默认的学习率是稳妥的

   关于损失函数的选择，需要注意，直接优化衡量问题成功的指标不一定总是可行的。有时 难以将指标转化为损失函数，要知道，损失函数需要在只有小批量数据时即可计算,而且还必须是可微的（否则无法用反向 传播来训练网络）。例如，广泛使用的分类指标 ROC AUC 就不能被直接优化。因此在分类任务 中，常见的做法是优化 ROC AUC 的替代指标，比如交叉熵。一般来说，你可以认为交叉熵越小， ROC AUC 越大

   

6. 扩大模型规模：开发过拟合的模型,一旦得到了具有统计功效的模型，问题就变成了：模型是否足够强大？它是否具有足够多 的层和参数来对问题进行建模？例如，只有单个隐藏层且只有两个单元的网络，在 MNIST 问题 上具有统计功效，但并不足以很好地解决问题。请记住，机器学习中无处不在的对立是优化和 泛化的对立，理想的模型是刚好在欠拟合和过拟合的界线上，要搞清楚你需要多大的模型，就必须开发一个过拟合的模型，

   1. 添加更多的层
   2. 让每一层变得更大
   3. 训练更多的轮次
   4. 要始终监控训练损失和验证损失，以及你所关心的指标的训练值和验证值。如果你发现模 型在验证数据上的性能开始下降，那么就出现了过拟合
   5. 下一阶段将开始正则化和调节模型，以便尽可能地接近理想模型，既不过拟合也不欠拟合

7. 模型正则化与调节超参数,这一步是最费时间的：你将不断地调节模型、训练、在验证数据上评估（这里不是测试数据）、 再次调节模型，然后重复这一过程，直到模型达到最佳性能,应该尝试以下几项:

   1. 添加 dropout
   2. 尝试不同的架构：增加或减少层数
   3. 添加 L1 和 / 或 L2 正则化
   4. 尝试不同的超参数（比如每层的单元个数或优化器的学习率），以找到最佳配置
   5. 反复做特征工程：添加新特征或删除没有信息量的特征
   6. 每次使用验证过程的反馈来调节模型，都会将有关验证过程的信息泄露到模型中。 如果只重复几次，那么无关紧要；但如果系统性地迭代许多次，最终会导致模型对验证过程过 拟合.这会降低验证过程的可靠性。

深度学习用于计算机视觉

深度学习在视觉上的应用主要是基于卷积神经网络，

卷积神经网络

卷积神经网络，convnet，CNN，下面是一个简单的CNN模型搭建：

重要的是，卷积神经网络接收形状为 (image_height, image_width, image_channels) 的输入张量（不包括批量维度）。本例中设置卷积神经网络处理大小为 (28, 28, 1) 的输入张量， 这正是 MNIST 图像的格式。我们向第一层传入参数 input_shape=(28, 28, 1) 来完成此设置

可以看模型的summary

可以看到，每个 Conv2D 层和 MaxPooling2D 层的输出都是一个形状为 (height, width, channels) 的 3D 张量。宽度和高度两个维度的尺寸通常会随着网络加深而变小。通道数量由传 入 Conv2D 层的第一个参数所控制（32 或 64）。

下一步是将最后的输出张量［大小为 (3, 3, 64)］输入到一个密集连接分类器网络中， 即 Dense 层的堆叠，

这些分类器可以处理 1D 向量，而当前的输出是 3D 张量。 首先，我们需要将 3D 输出展平为 1D，然后在上面添加几个 Dense 层：

这里Flatten()层的用法就是用来将输入“压平”，即把多维的输入一维化，常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小。

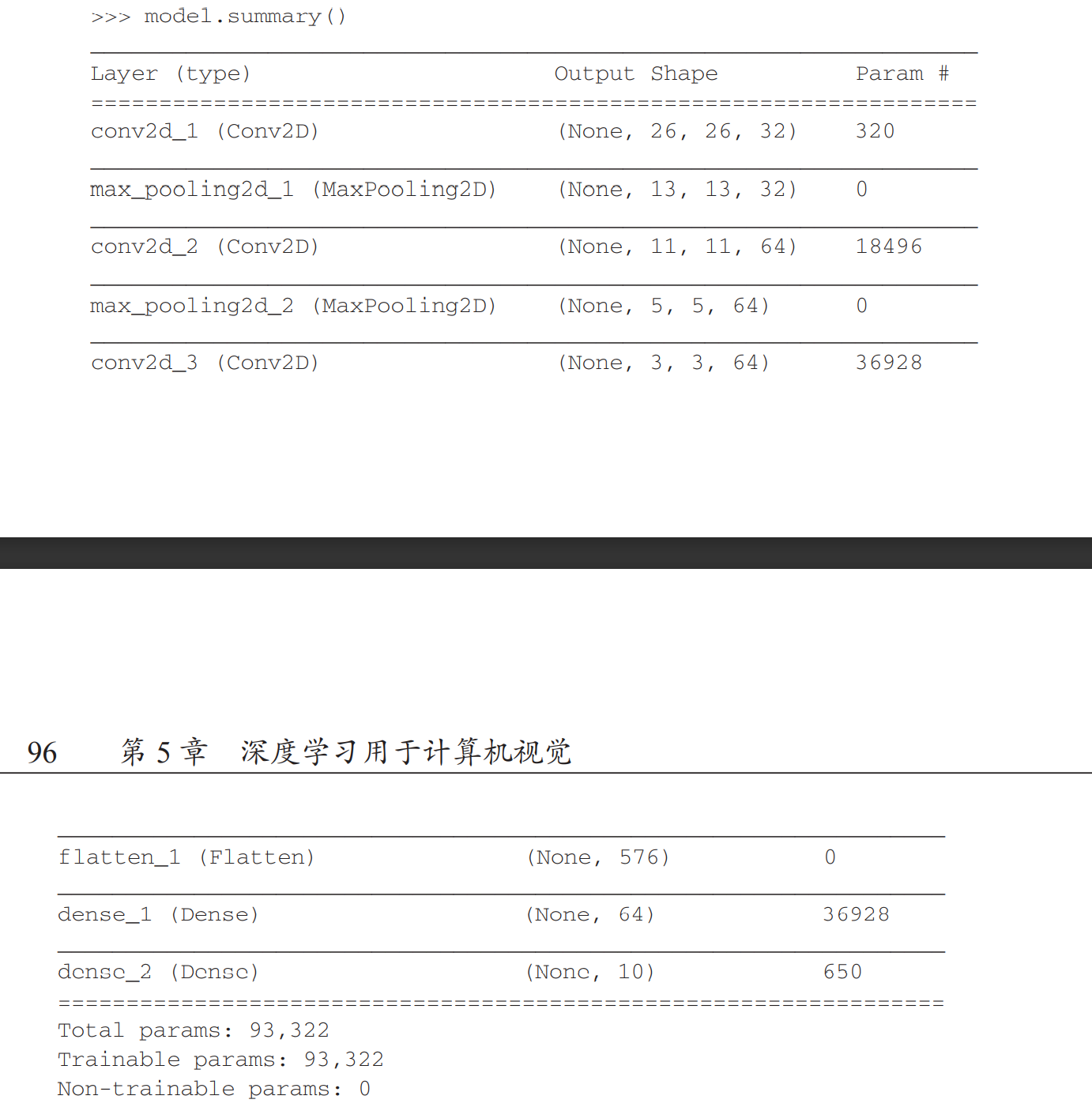
在进入两个 Dense 层之前，形状 (3, 3, 64) 的输出被展平为形状 (576,) 的 向量。

密集连接层和卷积层的根本区别在于，Dense 层从输入特征空间中学到的是全局模式，而卷积层学到的是局部模式，对于图像来说，学到的就是在输入图像的二维小窗口中发现的模式

这个重要特性使卷积神经网络具有以下两个有趣的性质：

1. 卷积神经网络学到的模式具有平移不变性，卷积神经网络在图像 右下角学到某个模式之后，它可以在任何地方识别这个模式，比如左上角。对于密集连 接网络来说，如果模式出现在新的位置，它只能重新学习这个模式。这使得卷积神经网 络在处理图像时可以高效利用数据（因为视觉世界从根本上具有平移不变性），它只需 要更少的训练样本就可以学到具有泛化能力的数据表示。
2. 卷积神经网络可以学到模式的空间层次结构,第一个卷积层将学习较小的局部模式（比如边缘），第二个卷积层将学习由第一层特征 组成的更大的模式，以此类推。这使得卷积神经网络可以有效地学习越来越复杂、越来 越抽象的视觉概念（因为视觉世界从根本上具有空间层次结构）

对于包含两个空间轴（高度和宽度）和一个深度轴（也叫通道轴）的 3D 张量，其卷积也 叫特征图,对于 RGB 图像，深度轴的维度大小等于 3，因为图像有 3 个颜色通道： 红色、绿色和蓝色,对于黑白图像（比如 MNIST 数字图像），深度等于 1（表示灰度等级）,卷 积运算从输入特征图中提取图块，并对所有这些图块应用相同的变换，生成输出特征图,该输出特征图仍是一个 3D 张量，具有宽度和高度，其深度可以任意取值，因为 输出深度是层的参数，深度轴的不同通道不再像 RGB 输入那样代表特定颜色，而是代表过滤器，过滤器对输入数据的某一方面进行编码

MNIST 示例中，第一个卷积层接收一个大小为 (28, 28, 1) 的特征图，并输出一个大 小为 (26, 26, 32) 的特征图，即它在输入上计算 32 个过滤器。对于这 32 个输出通道，每个 通道都包含一个 26×26 的数值网格，它是过滤器对输入的响应图，表示这个过 滤器模式在输入中不同位置的响应，这也是特征图这一术语的含义：深度轴的每个 维度都是一个特征（或过滤器），而 2D 张量 output[:, :, n] 是这个过滤器在输入上的响应 的二维空间图

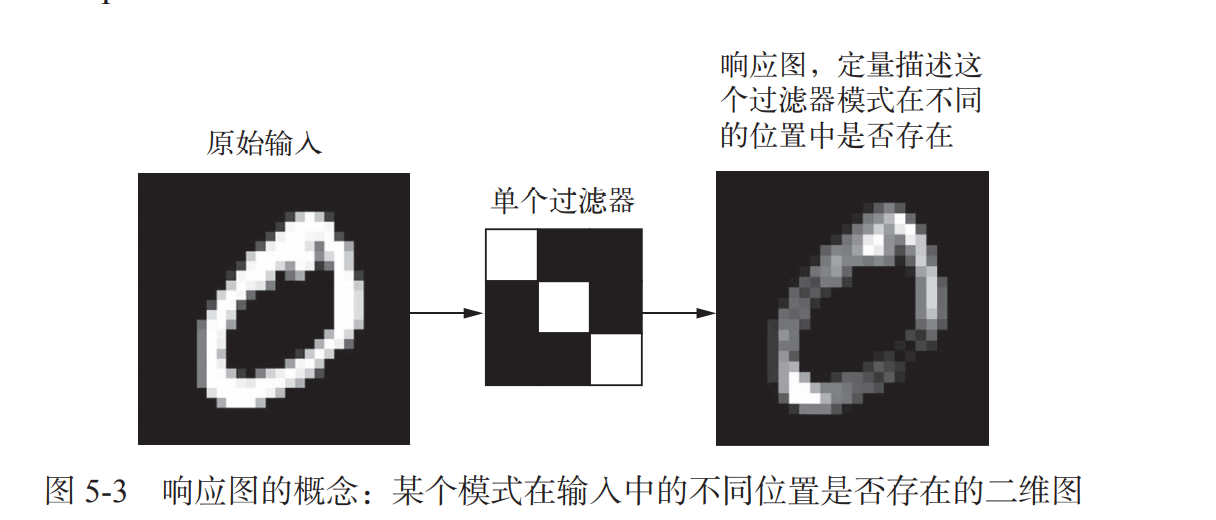
卷积由以下两个关键参数所定义：

1. 从输入中提取的图块尺寸：这些图块的大小通常是 3×3 或 5×5。
2. 输出特征图的深度：卷积所计算的过滤器的数量。

对于 Keras 的 Conv2D 层，这些参数都是向层传入的前几个参数：Conv2D(output_depth, (window_height, window_width))。

卷积的工作原理：在 3D 输入特征图上滑动（slide）这些 3×3 或 5×5 的窗口，在每个可能 的位置停止并提取周围特征的 3D 图块［形状为 (window_height, window_width, input_ depth)］。然后每个 3D 图块与学到的同一个权重矩阵［叫作卷积核]做 张量积，转换成形状为 (output_depth,) 的 1D 向量,然后对所有这些向量进行空间重组， 使其转换为形状为 (height, width, output_depth) 的 3D 输出特征图。输出特征图中的 每个空间位置都对应于输入特征图中的相同位置

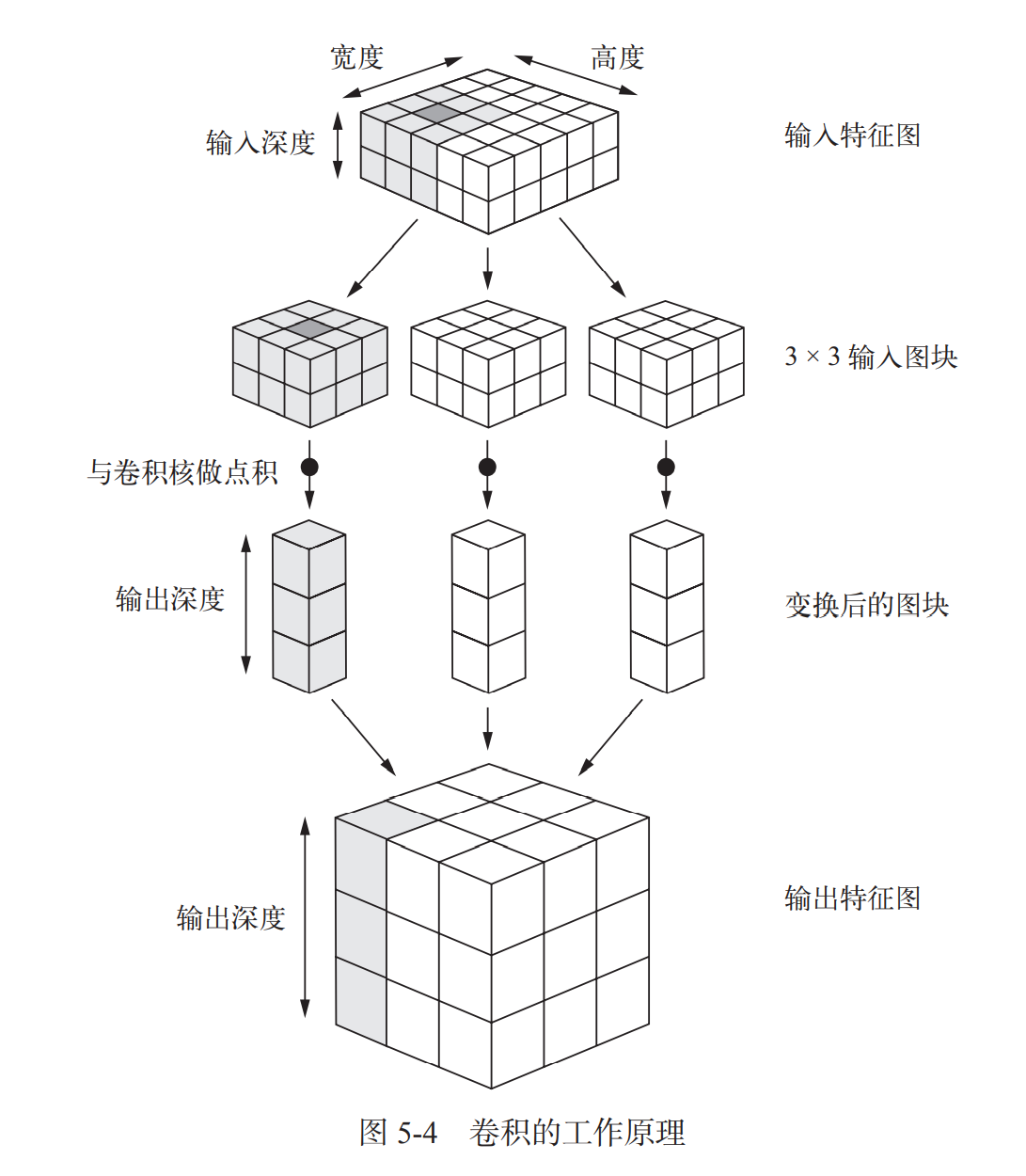
• 边界效应与填充

假设有一个 5×5 的特征图（共 25 个方块）。其中只有 9 个方块可以作为中心放入一个 3×3 的窗口，这 9 个方块形成一个 3×3 的网格（见图 5-5）。因此，输出特征图的尺寸是 3×3。 它比输入尺寸小了一点,如果你希望输出特征图的空间维度与输入相同，那么可以使用填充（padding）。填充是在 输入特征图的每一边添加适当数目的行和列，使得每个输入方块都能作为卷积窗口的中心

于 3×3 的窗口，在左右各添加一列，在上下各添加一行。对于 5×5 的窗口，各添加两行和两列

对于 Conv2D 层，可以通过 padding 参数来设置填充，这个参数有两个取值：”valid” 表 示不使用填充（只使用有效的窗口位置）；”same” 表示“填充后输出的宽度和高度与输入相同”。 padding 参数的默认值为 “valid”

• 卷积步幅

影响输出尺寸的另一个因素是步幅的概念。目前为止，对卷积的描述都假设卷积窗口的中 心方块都是相邻的。但两个连续窗口的距离是卷积的一个参数，叫作步幅，默认值为 1，也可 以使用步进卷积，即步幅大于 1 的卷积步幅为 2 意味着特征图的宽度和高度都被做了 2 倍下采样（除了边界效应引起的变化）。虽 然步进卷积对某些类型的模型可能有用，但在实践中很少使用，为了对特征图进行下采样，我们不用步幅，而是通常使用最大池化

• 最大池化运算

在每个 MaxPooling2D 层之后，特征图的尺寸都 会减半，最大池化的作用：对特征图进行下采样，与步进卷积类似，最大池化是从输入特征图中提取窗口，并输出每个通道的最大值，但是最大池化使用硬编码的 max 张量运算对局部图块进行变换，而不是使用学到的线性变换,最大池化与卷积的最大不同之处在于，最大池化通常使用 2×2 的窗口和步幅 2，其目 的是将特征图下采样 2 倍。与此相对的是，卷积通常使用 3×3 窗口和步幅 1

简而言之，使用下采样的原因，一是减少需要处理的特征图的元素个数，二是通过让连续 卷积层的观察窗口越来越大（即窗口覆盖原始输入的比例越来越大），从而引入空间过滤器的层 级结构。

小型卷积神经网络的搭建

这里用一个猫狗分类的模型来进行示例，完整展示开发流程：

首先是对数据集的处理：

def get_pic():
    print("划分训练集测试集")
    path = './data/dogs-vs-cats/train'
    main_path = './data/dvsc'
    os.mkdir(main_path)
    #训练数据集划分
    trian_dir = os.path.join(main_path,'train')
    os.mkdir(trian_dir)
    #测试集
    test_dir = os.path.join(main_path,'test')
    os.mkdir(test_dir)
    #验证集
    val_dir = os.path.join(main_path,'val')
    os.mkdir(val_dir)
    #分别训练集
    train_cat_dir = os.path.join(trian_dir,'cat')
    os.mkdir(train_cat_dir)
    train_dog_dir = os.path.join(trian_dir,'dog')
    os.mkdir(train_dog_dir)
    #分别测试集
    test_cat_dir = os.path.join(test_dir,'cat')
    os.mkdir(test_cat_dir)
    test_dog_dir = os.path.join(test_dir,'dog')
    os.mkdir(test_dog_dir)
    #分别验证集
    val_cat_dir = os.path.join(val_dir,'cat')
    os.mkdir(val_cat_dir)
    val_dog_dir = os.path.join(val_dir,'dog')
    os.mkdir(val_dog_dir)
    #复制图片到对应目录
    #猫训练1000张
    fnames=['cat.{}.jpg'.format(i) for i in range(1000)]
    for fname in fnames:
        src = os.path.join(path,fname)
        dir = os.path.join(train_cat_dir,fname)
        shutil.copyfile(src,dir)

    #狗训练1000张
    fnames=['dog.{}.jpg'.format(i) for i in range(1000)]
    for fname in fnames:
        src = os.path.join(path,fname)
        dir = os.path.join(train_dog_dir,fname)
        shutil.copyfile(src,dir)

    #猫测试500张
    fnames=['cat.{}.jpg'.format(i) for i in range(1000,1500)]
    for fname in fnames:
        src = os.path.join(path,fname)
        dir = os.path.join(test_cat_dir,fname)
        shutil.copyfile(src,dir)
    #狗测试500张
    fnames=['dog.{}.jpg'.format(i) for i in range(1000,1500)]
    for fname in fnames:
        src = os.path.join(path,fname)
        dir = os.path.join(test_dog_dir,fname)
        shutil.copyfile(src,dir)
    #猫验证500
    fnames=['cat.{}.jpg'.format(i) for i in range(1500,2000)]
    for fname in fnames:
        src = os.path.join(path,fname)
        dir = os.path.join(val_cat_dir,fname)
        shutil.copyfile(src,dir)
    #狗验证500
    fnames=['dog.{}.jpg'.format(i) for i in range(1500,2000)]
    for fname in fnames:
        src = os.path.join(path,fname)
        dir = os.path.join(val_dog_dir,fname)
        shutil.copyfile(src,dir)

划分了训练集，测试集，验证集，接下来进行模型的搭建

网络中特征图的深度在逐渐增大（从 32 增大到 128），而特征图的尺寸在逐渐减小（从 150×150 减小到 7×7）。这几乎是所有卷积神经网络的模式。

因为是一个二分类问题，所以网络最后一层是使用 sigmoid 激活的单一单元（大小为 1 的 Dense 层）。这个单元将对某个类别的概率进行编码

进行模型定义：

def model_build():
    model = models.Sequential()
    #第一层为输出channels为32，(3,3)指明 2D 卷积窗口的宽度和高度为3，输入为高，宽150x150,3通道（RGB）三原色通道
    model.add(layers.Conv2D(32,(3,3),activation='relu',input_shape=(150,150,3)))
    #最大池化
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Conv2D(64,(3,3),activation='relu'))
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Conv2D(128,(3,3),activation='relu'))
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Conv2D(128,(3,3),activation='relu'))
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Flatten())
    model.add(layers.Dense(512,activation='relu'))
    model.add(layers.Dense(1,activation='sigmoid'))
    model.compile(loss='binary_crossentropy',optimizer=optimizers.RMSprop(lr=1e-4),metrics=['acc'])

接下来需要对数据集进行处理，数据集是jpeg格式的图片，需要将其转化为浮点型的张量，进行数据预处理包括：

(1) 读取图像文件。

(2) 将 JPEG 文件解码为 RGB 像素网格

(3) 将这些像素网格转换为浮点数张量

(4) 将像素值（0~255 范围内）缩放到 [0, 1] 区间（神经网络适合处理较小的输入值）

在keras中，有对应的图像处理api：keras.preprocessing.image

特别地，它包含 ImageDataGenerator 类，可以快速创建 Python 生成器，能够将硬盘上的图像文件自动转换 为预处理好的张量批量、

def image_handle():
    """
    数据预处理
    :return:
    """
    #图像缩放255倍
    train_datagen = ImageDataGenerator(rescale=1./255)
    test_datagen = ImageDataGenerator(rescale=1./255)
    main_path = './data/dvsc'
    train_dir = os.path.join(main_path,'train')
    test_dir = os.path.join(main_path,'test')
    val_dir = os.path.join(main_path,'val')
    train_generator = ImageDataGenerator.flow_from_directory(
        train_dir,
        #大小调整为150x150
        target_size=(150,150),
        batch_size=20,
        class_mode='binary'
    )
    val_generator = ImageDataGenerator.flow_from_directory(
        val_dir,
        target_size=(150,150),
        batch_size=20,
        class_mode='binary'
    )
    model = model_build()
    model.fit_generator(
        train_generator,
        steps_per_epoch=100,
        epochs=30,
        validation_data=val_generator,
        validation_steps=50
    )
        #保存模型
    model.save('cat_or_dog_test1.h5')

利用生成器，我们让模型对数据进行拟合。我们将使用 fit_generator 方法来拟合，它 在数据生成器上的效果和 fit 相同。它的第一个参数应该是一个 Python 生成器，可以不停地生 成输入和目标组成的批量，比如 train_generator。因为数据是不断生成的，所以 Keras 模型 要知道每一轮需要从生成器中抽取多少个样本。这是 steps_per_epoch 参数的作用：从生成 器中抽取 steps_per_epoch 个批量后（即运行了 steps_per_epoch 次梯度下降），拟合过程 将进入下一个轮次。本例中，每个批量包含 20 个样本，所以读取完所有 2000 个样本需要 100 个批量。

使用 fit_generator 时，你可以传入一个 validation_data 参数，其作用和在 fit 方 法中类似。值得注意的是，这个参数可以是一个数据生成器，但也可以是 Numpy 数组组成的元 组。如果向 validation_data 传入一个生成器，那么这个生成器应该能够不停地生成验证数 据批量，因此你还需要指定 validation_steps 参数，说明需要从验证生成器中抽取多少个批 次用于评估。

在经历上述模型的训练后，明显有出过拟合的特征。训练精度随着时间线性增加，直到接近 100%，而验 证精度则停留在 70%~72%。验证损失仅在 5 轮后就达到最小值，然后保持不变，而训练损失则 一直线性下降，直到接近于 0

前面已经介绍过几种 降低过拟合的技巧，比如 dropout 和权重衰减（L2 正则化）。现在我们将使用一种针对于计算 机视觉领域的新方法，在用深度学习模型处理图像时几乎都会用到这种方法，它就是数据增强

数据增强

过拟合的原因是学习样本太少，导致无法训练出能够泛化到新数据的模型。如果拥有无限 的数据，那么模型能够观察到数据分布的所有内容，这样就永远不会过拟合。数据增强是从现 有的训练样本中生成更多的训练数据，其方法是利用多种能够生成可信图像的随机变换来增加样本 ，。其目标是，模型在训练时不会两次查看完全相同的图像。这让模型能够观察 到数据的更多内容，从而具有更好的泛化能力

在 Keras 中，这可以通过对 ImageDataGenerator 实例读取的图像执行多次随机变换来实现，直接通过例子来看：

datagen = ImageDataGenerator(
    rotation_range=40,
     width_shift_range=0.2,
     height_shift_range=0.2,
     shear_range=0.2,
     zoom_range=0.2,
     horizontal_flip=True,
     fill_mode='nearest'
     )

• rotation_range 是角度值（在 0~180 范围内），表示图像随机旋转的角度范围
• width_shift 和 height_shift 是图像在水平或垂直方向上平移的范围（相对于总宽 度或总高度的比例）
• shear_range 是随机错切变换的角度
• zoom_range 是图像随机缩放的范围。
• horizontal_flip 是随机将一半图像水平翻转。如果没有水平不对称的假设（比如真 实世界的图像），这种做法是有意义的
• fill_mode是用于填充新创建像素的方法，这些新像素可能来自于旋转或宽度/高度平移。

增强后的图像示例：

使用这种数据增强来训练一个新网络，那么网络将不会两次看到同样的输入。但网 络看到的输入仍然是高度相关的，因为这些输入都来自于少量的原始图像。无法生成新信息， 而只能混合现有信息。因此，这种方法可能不足以完全消除过拟合。为了进一步降低过拟合， 你还需要向模型中添加一个 Dropout 层，添加到密集连接分类器之前。：

model = models.Sequential()
    #第一层为输出channels为32，(3,3)指明 2D 卷积窗口的宽度和高度为3，输入为高，宽150x150,3通道（RGB）三原色通道
    model.add(layers.Conv2D(32,(3,3),activation='relu',input_shape=(150,150,3)))
    #最大池化
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Conv2D(64,(3,3),activation='relu'))
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Conv2D(128,(3,3),activation='relu'))
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Conv2D(128,(3,3),activation='relu'))
    model.add(layers.MaxPool2D((2,2)))
    model.add(layers.Flatten())
    model.add(layers.Dropout(0.5))    #添加dropout层
    model.add(layers.Dense(512,activation='relu'))
    model.add(layers.Dense(1,activation='sigmoid'))
    model.compile(loss='binary_crossentropy',optimizer=optimizers.RMSprop(lr=1e-4),metrics=['acc'])

# train_datagen = ImageDataGenerator(rescale=1./255)
   #数据增强，但不能对验证集数据进行增强
   train_datagen = ImageDataGenerator(
       rescale=1./255,
       rotation_range=40,
       width_shift_range=0.2,
       height_shift_range=0.2,
       shear_range=0.2,
       zoom_range=0.2,
       horizontal_flip=True,
       fill_mode='nearest'
   )

这样就可以减少过拟合，提高准确率

使用预训练的卷积神经网络

预训练网络，是一个保存好的网络，之前已在大型数据集（通常是大规模图 像分类任务）上训练好。如果这个原始数据集足够大且足够通用，那么预训练网络学到的特征 的空间层次结构可以有效地作为视觉世界的通用模型，即使这些新问题涉及的类别和原始任务完全不同，

使用预训练网络有两种方法：特征提取（feature extraction）和微调模型（fine-tuning）

特征提取

特征提取是使用之前网络学到的表示来从新样本中提取出有用的特征。然后将这些特征输 入一个新的分类器，从头开始训练。

用于图像分类的卷积神经网络包含两部分：首先是一系列池化层和卷积层，最 后是一个密集连接分类器。第一部分叫作模型的卷积基，对于卷积神经网 络而言，特征提取就是取出之前训练好的网络的卷积基，在上面运行新数据，然后在输出上面 训练一个新的分类器

原因在于卷积基学到的表示可能更加通用，因此更适合重复使用。卷积神经网络的特征 图表示通用概念在图像中是否存在，无论面对什么样的计算机视觉问题，这种特征图都可能很 有用

注意，某个卷积层提取的表示的通用性（以及可复用性）取决于该层在模型中的深度。模型中更靠近底部的层提取的是局部的、高度通用的特征图（比如视觉边缘、颜色和纹理），而更 靠近顶部的层提取的是更加抽象的概念（比如“猫耳朵”或“狗眼睛”）因此，如果新数据集与原始模型训练的数据集有很大差异，那么最好只使用模型的前几层来做特征提取，而不 是使用整个卷积基。

这里更靠近底部的层是指在定义模型时先添加到模型中的层，而更靠近顶部的层则是后添加到模型中的层，下同

使用在 ImageNet 上训练的 VGG16 网络的卷积基从 猫狗图像中提取有趣的特征，然后在这些特征上训练一个猫狗分类器，VGG16 等模型内置于 Keras 中，可以从 keras.applications 模块中导入。下面是 keras.applications 中的一部分图像分类模型（都是在 ImageNet 数据集上预训练得到的）

大创做完了，就这还升级了，我是真不想搞啊。。。鸽了鸽了